Table of Contents
The Wilcoxon Signed Rank Test is a non-parametric test used to compare two related samples or repeated measurements on a single sample. To perform this test in Excel, one must first organize the data into two columns, one with the pre-test scores and the other with the post-test scores. Then, the Data Analysis tool should be used to select the Wilcoxon Signed Rank Test option. This will generate a result table which should be interpreted to determine whether there is a significant difference between the two samples.
The is the non-parametric version of the .
It is used to test whether or not there is a significant difference between two population means when the distribution of the differences between the two samples cannot be assumed to be .
This tutorial provides a step-by-step example of how to conduct a Wilcoxon Signed-Rank Test in Excel.
Step 1: Create the Data
Suppose an engineer want to know if a new fuel treatment leads to a change in the average miles per gallon of a certain car. To test this, he measures the mpg of 12 cars with and without the fuel treatment.
We’ll create the following data in Excel to hold the mpg values for each car with the fuel treatment (group1) and without the fuel treatment (group 2):

Step 2: Calculate the Difference Between the Groups
Next, we’ll calculate the difference between the groups:
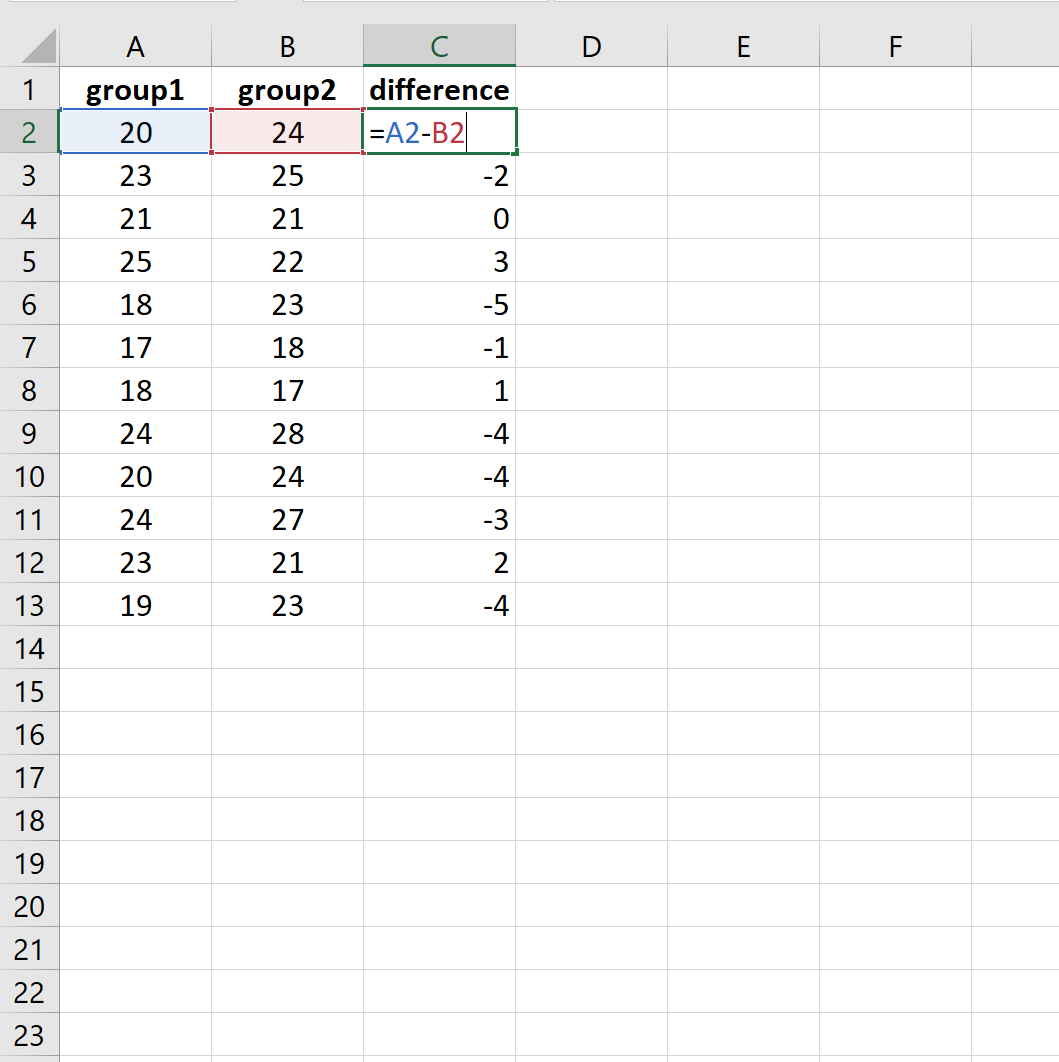
Step 3: Calculate the Absolute Differences
Next, we’ll calculate the absolute difference between the groups, returning a blank if the absolute difference is zero:

Step 4: Calculate the Rank of the Absolute Differences
Next, we’ll use the RANK.AVG() function to calculate the rank of the absolute differences between the groups, returning a blank if the absolute difference is zero:
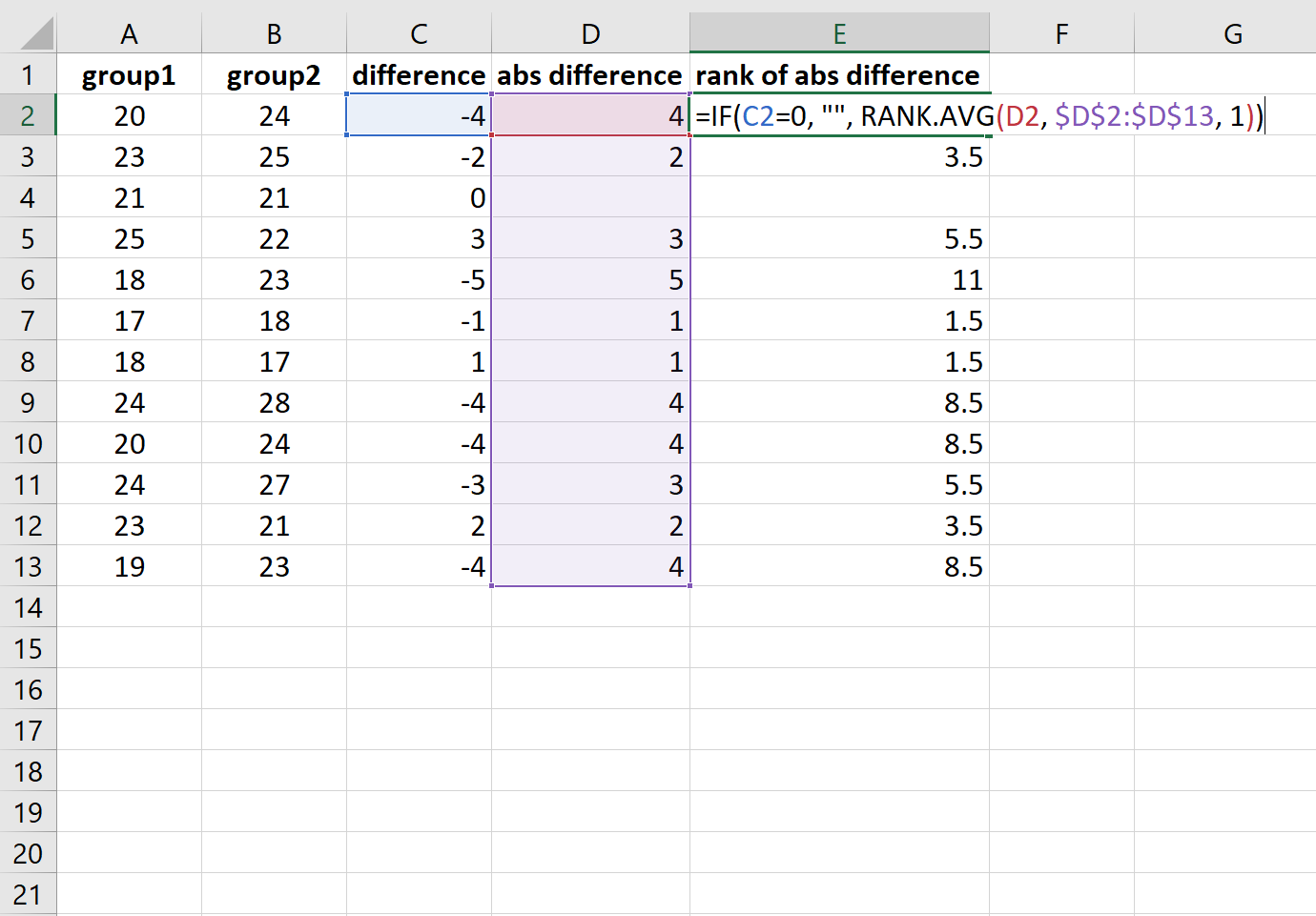
Step 5: Calculate the Positive & Negative Ranks

And we’ll calculate the negative ranks:

Step 6: Calculate the Test Statistic & Sample Size
Lastly, we’ll calculate the test statistic which is simply the smaller of the sum of the positive ranks or the sum of the negative ranks:
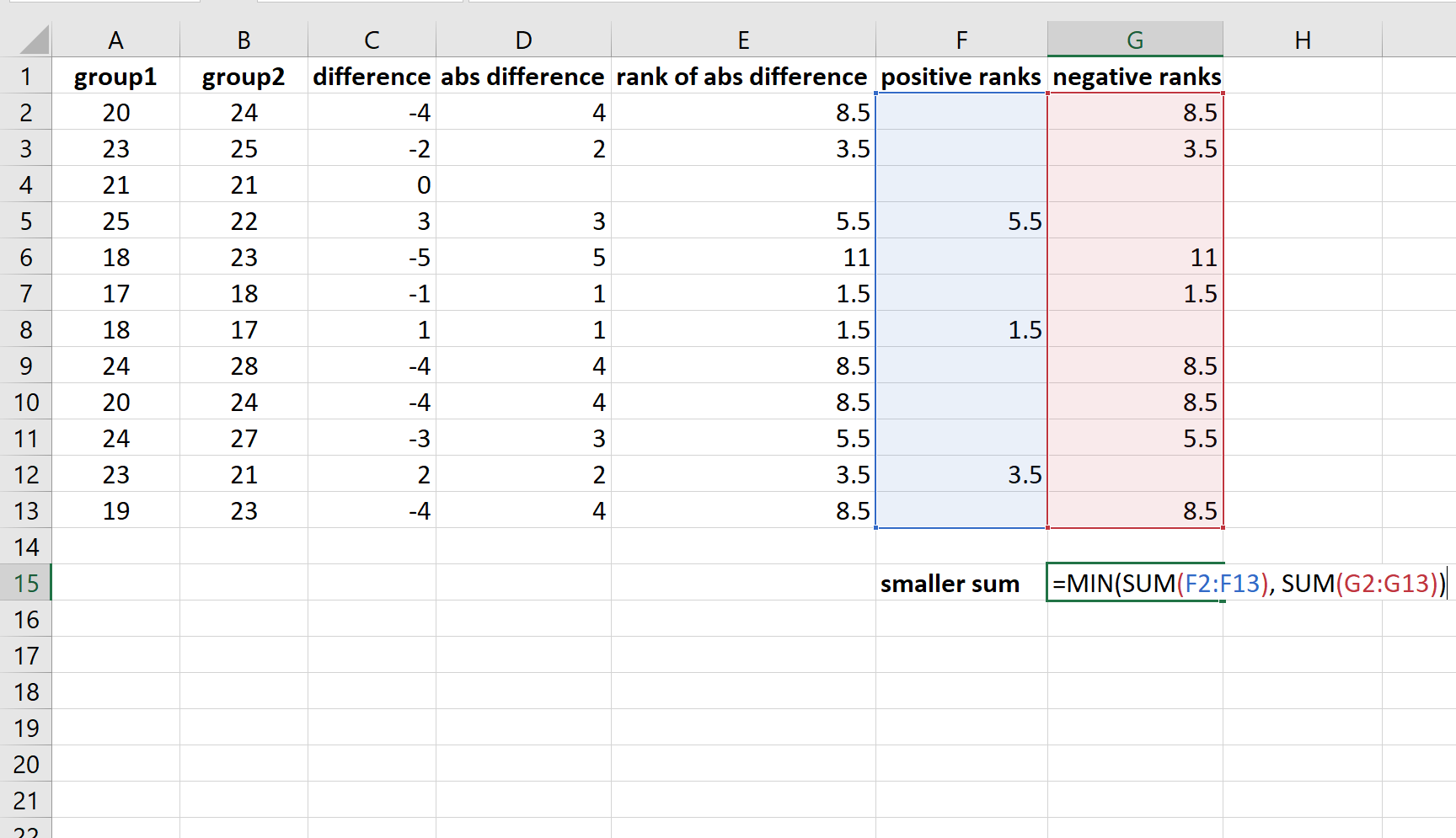
And we’ll calculate the sample size, which is the total number of ranks that aren’t equal to zero:
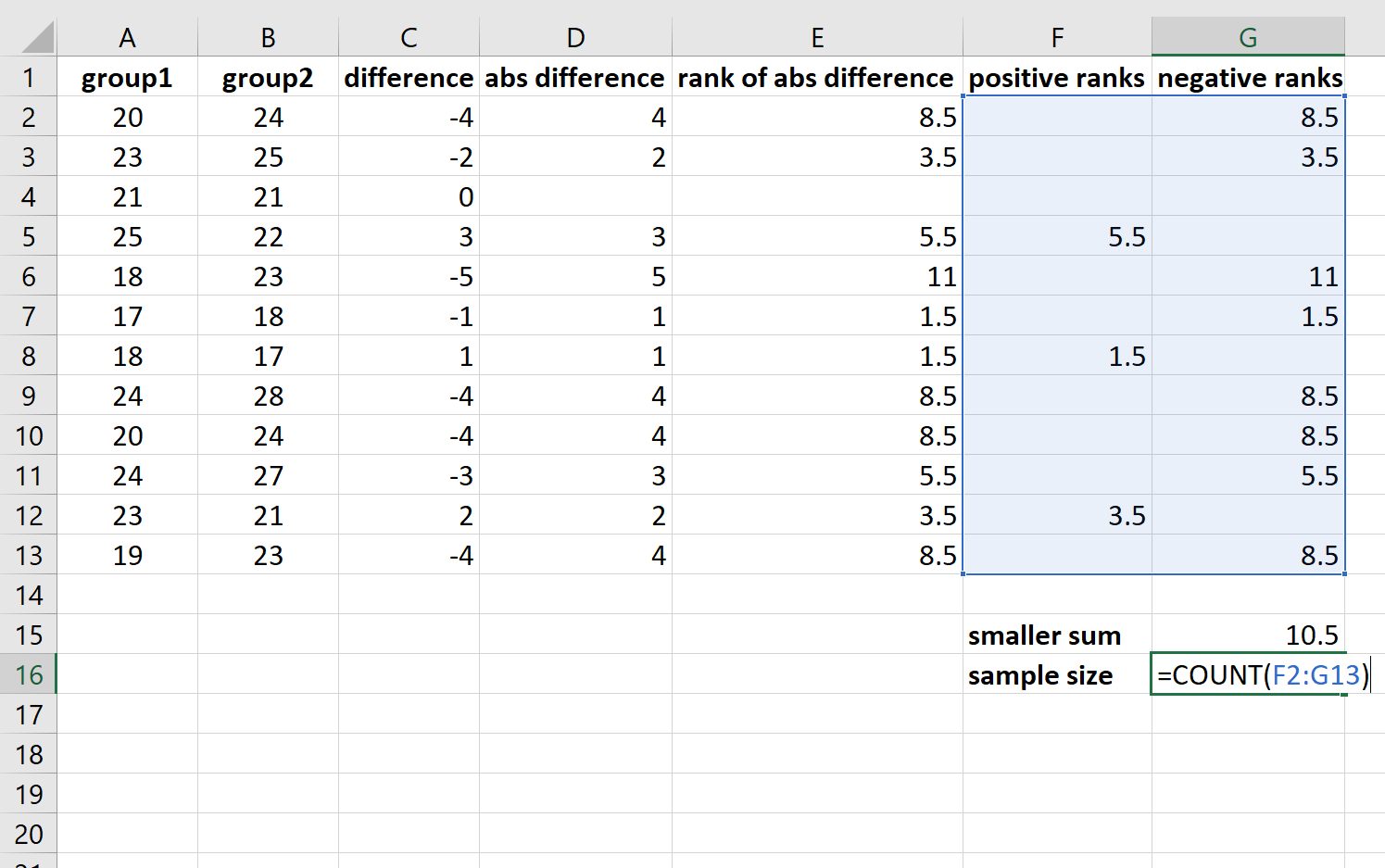
The test statistic turns out to be 10.5 and the sample size is 11.
In this example, the Wilcoxon Signed-Rank Test uses the following null and alternative hypotheses:
H0: The mpg is equal between the two groups
HA: The mpg is not equal between the two groups
To determine if we should reject or fail to reject the null hypothesis, we can find the critical value that corresponds to α = .05 and a sample size of 11 in the following Wilcoxon Signed Rank Test Critical Values Table:
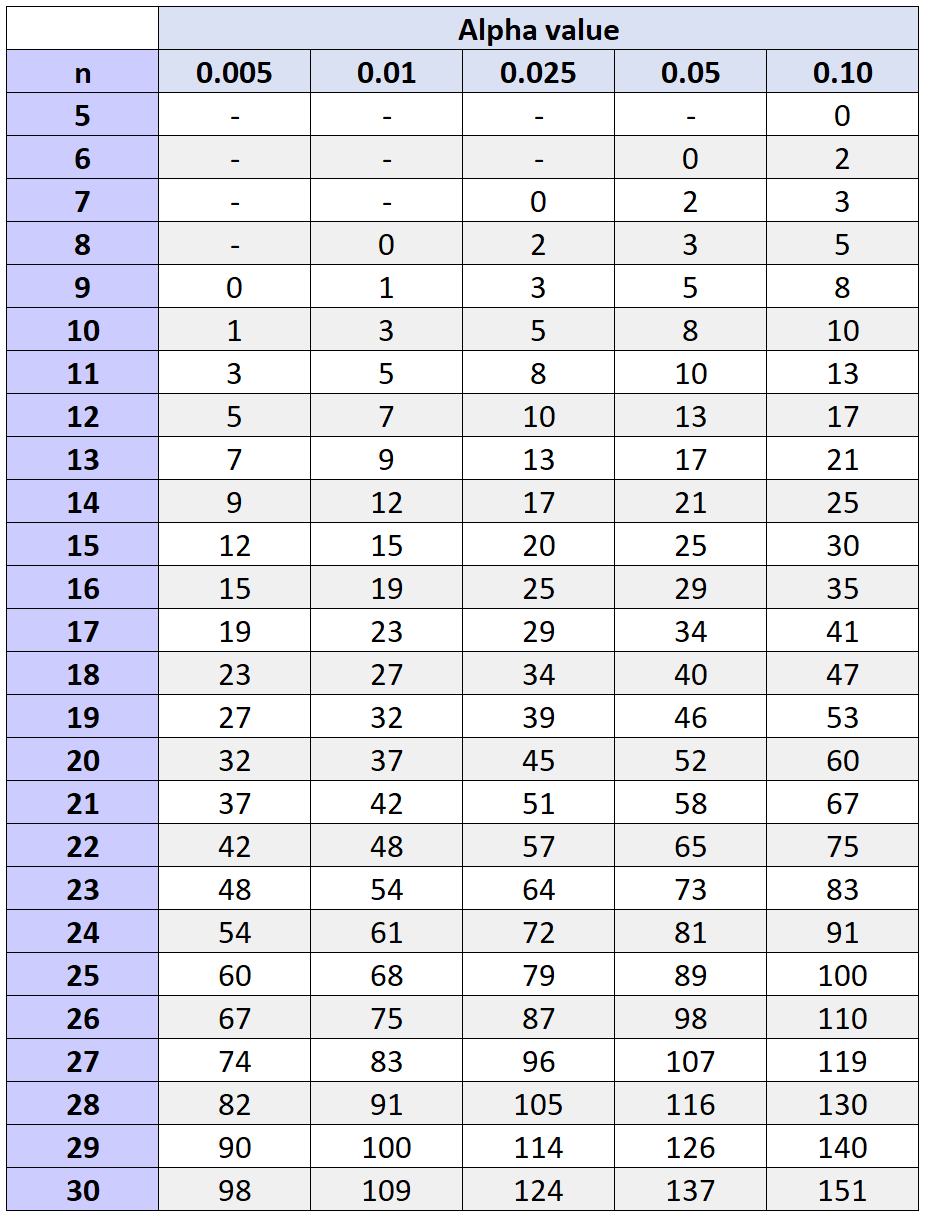
The critical value that corresponds to α = .05 and a sample size of 11 is 10.
Since the test statistic (10.5) is not less than the critical value of 10, we fail to reject the null hypothesis.
We do not have sufficient evidence to say that the mean mpg is not equal between the two groups.
Bonus: Feel free to use this to automatically calculate the test statistic for a Wilcoxon Signed-Rank Test.
