Table of Contents
The G-Test of Goodness of Fit is a statistical test used to determine if a given set of data follows a specific distribution or pattern. It is often used to analyze categorical data and compare it to an expected distribution. This test calculates the differences between the observed and expected values and determines if they are statistically significant. It is a useful tool for evaluating the fit of a model or hypothesis to a set of data and can provide valuable insights into the underlying patterns and relationships within the data. It is commonly used in fields such as biology, social sciences, and market research.
What is the G-Test of Goodness of Fit?
The G-Test of Goodness of Fit is a statistical test used to determine if the proportions of categories in a single qualitative variable significantly differ from an expected or known population proportion. It can also be used to compare two sample proportions. To use it, you should have one group variable with two or more options and you should have more than 10 values in every cell and more than 1000 observations in total. See more below.
The G-Test of Goodness of Fit is also called the G-Test, Likelihood Ratio Test, the Log-Likelihood Ratio Test.
Assumptions for the G-Test of Goodness of Fit
Every statistical method has assumptions. Assumptions mean that your data must satisfy certain properties in order for statistical method results to be accurate.
The assumptions for the G-Test of Goodness of Fit include:
- Random Sample
- Sample Size
- Mutually Exclusive
Let’s dive into what that means.
Random Sample
The data points for each group in your analysis must have come from a simple random sample. This means that if you want to know if your sample of people has a different ratio of Male/Female than the population, then the sample should be randomly selected. This is important because if your groups were not randomly determined then your analysis will be incorrect. In statistical terms this is called bias, or a tendency to have incorrect results because of bad data.
Sample Size
Each option in your group should have more than 10 subjects/participants. This means if you sampled men and women, you should have at least 10 men and at least 10 women.
Mutually Exclusive
No subject or participant should be included under both conditions. Each row in your data should only be included in a single group.
When to use the G-Test of Goodness of Fit?
You should use the G-Test of Goodness of Fit in the following scenario:
- You want to know the difference between two variables
- Your variable of interest is proportional or categorical
- You have two or more options
- You have more than 10 in each cell and more than 1000 observations overall
Let’s clarify these to help you know when to use the G-Test of Goodness of Fit.
Difference
You are looking for a statistical test to look at how a variable differs between two groups. Other types of analyses include testing for a relationship between two variables or predicting one variable using another variable (prediction).
Proportional or Categorical
For this test, your variable of interest must be proportional or categorical. A categorical variable is a variable that contains categories without a natural order. Examples of categorical variables are eye color, city of residence, type of dog, etc. Proportional variables are derived from categorical variables, for instance: the number of people that converted on two different versions of your website (10% vs 15%), percentages, the number of people who voted vs people who did not vote, the proportion of plants that died vs survived an experimental treatment, etc.
If you have a continuous variable that you want to compare to an expected population, you may want to use a Single Sample Z-Test.
Two or more Options
Your categorical variable should have two or more possible options. This could be a binary variable such as recovered from disease (yes/no), or it could have additional options like eye color (blue/brown/black/green)
If you have only than two options and fewer than 10 in a cell, you should consider using the Binomial Test
More than 10 in each Cell (and more than 1000 overall)
The rule-of-thumb we recommend is to use this test when you have around 10 or more observations in each cell. “Cell” in this case refers simply to the count of values in each group. For example, if I have a list of survey responses with 5 “yes” and 1 “no”, there are 5 and 1 value(s) per cell, respectively.
In addition, we recommend using this test when you have more than 1000 observations overall.
If you have less than 10 in a cell, we recommend using the Binomial Test if you have only two options in your group variable or the Multinomial Goodness-of-Fit Test if you have more than two. And if you have more than 10 in every cell but fewer than 1000 total observations, we recommend using the One-Proportion Z-Test if you have only two options or the Chi-Square Goodness-of-Fit Test if you have more than two.
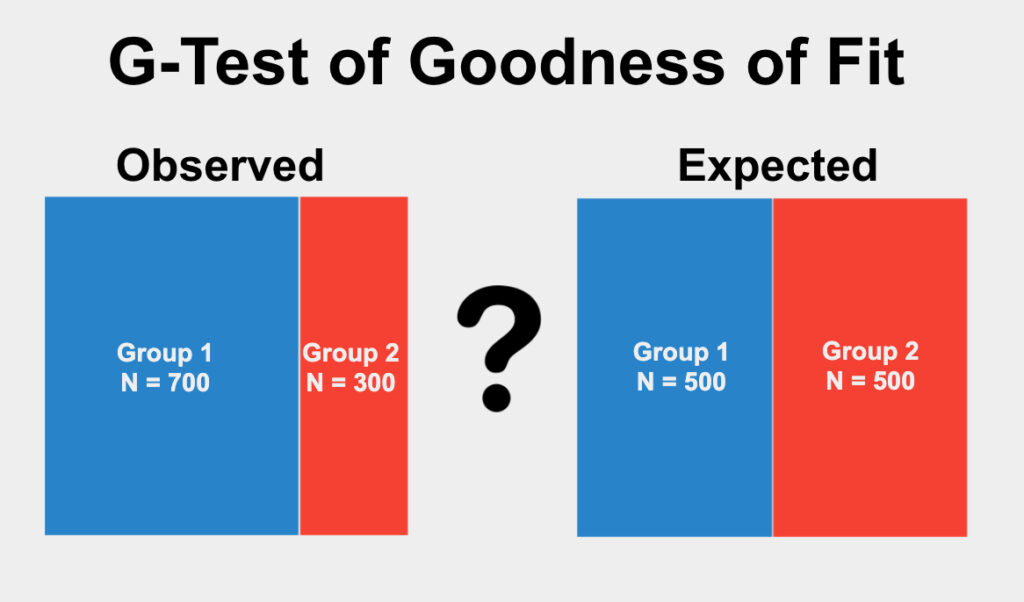
G-Test of Goodness of Fit Example
Variable: Gender (male/female)
In this example, we are interested in investigating whether our sample of subjects’ genders differ significantly from a known population proportion of 50-50. The null hypothesis is that there is no difference between the proportion of females (or males) in our sample. Because we have a random sample, our data points are independent, and our groups are mutually exclusive, we can proceed with the test.
The analysis will result in a G statistic and a p-value. The p-value represents the chance of seeing our results if there was an actual split of 50-50 in the population. A p-value less than or equal to 0.05 means that our result is statistically significant and we can trust that the difference is not due to chance alone.
