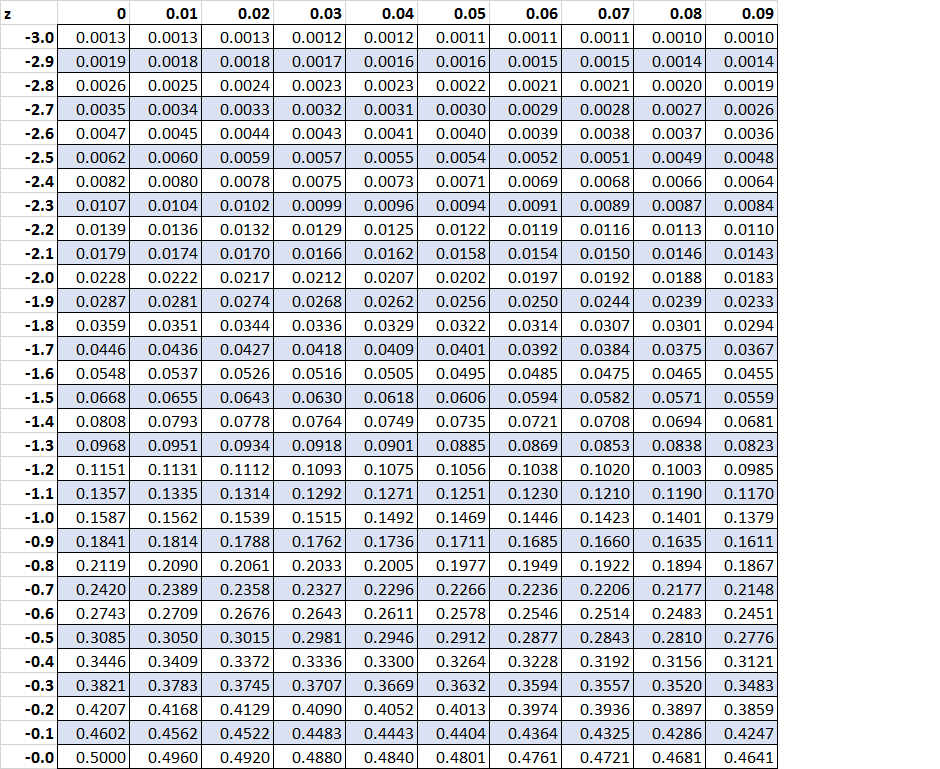
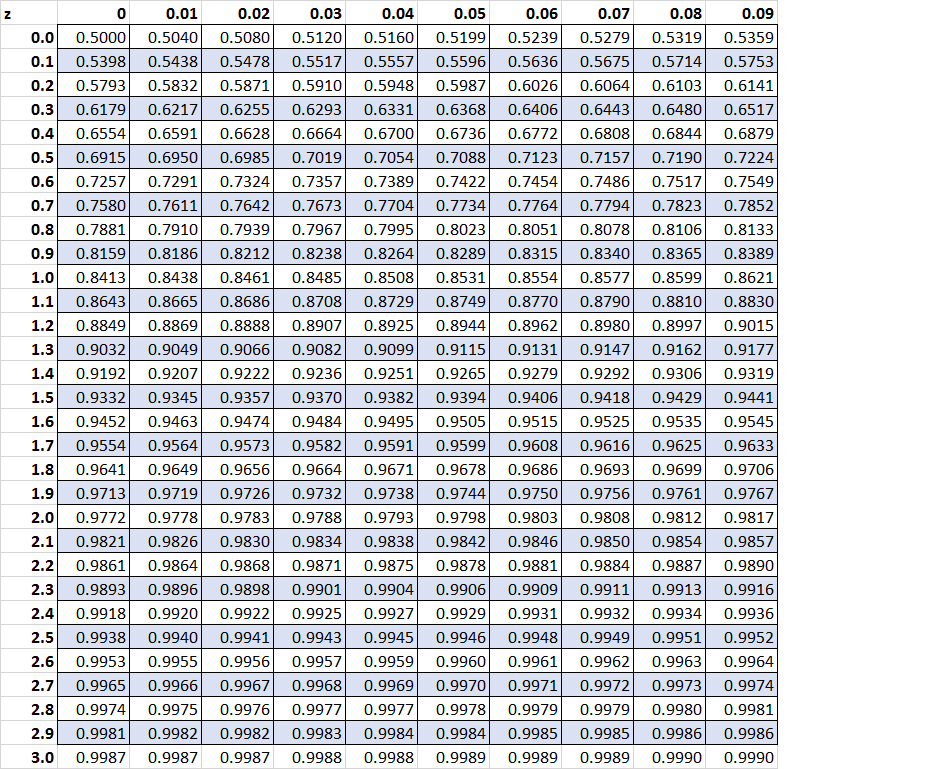
The Z-Table, also known as the standard normal distribution table, is a crucial tool in statistics for working with data that follows a normal distribution. It helps you find the probability of a certain value falling within a specific range under the standard normal curve. Here’s a breakdown of the Z-Table and its uses:
What it shows:
- The table displays the area under the standard normal curve to the left of a specific z-score. This z-score represents how many standard deviations a particular value is away from the mean (0) in the standard normal distribution.
- It features two sections: one for positive z-scores (values above the mean) and one for negative z-scores (values below the mean).
- Each section is further divided into rows and columns:
- Rows: Represent the first decimal place of the z-score (e.g., 0.0, 0.1, 0.2, etc.).
- Columns: Represent the second and third decimal places of the z-score (e.g., .00, .01, .02, etc.).
- The table entry at the intersection of a row and column corresponds to the area under the curve to the left of that specific z-score.
How to use it:
- Calculate the z-score of your data point: This involves subtracting the mean of your data from your individual value and then dividing by the standard deviation.
- Identify the appropriate section of the table: Positive for values above the mean, negative for values below.
- Locate the row and column corresponding to your calculated z-score.
- The table entry at that intersection represents the probability of a value falling to the left of your z-score under the standard normal curve.
Applications:
- Finding probabilities: You can use the Z-Table to calculate the probability of a specific value occurring in your data, given that it follows a normal distribution.
- Hypothesis testing: The Z-Table is essential for conducting hypothesis tests with normally distributed data, such as Z-tests for proportions or single means.
- Confidence intervals: You can use the Z-Table to construct confidence intervals for population parameters like the mean or proportion, based on sample data.