F Distribution Table

By /

The F Distribution Table, also known as the F-table, plays a crucial role in statistical analysis for conducting F-tests. These tests help compare variances between two or more groups, making them valuable tools in various fields like research and engineering. Here’s an explanation of the table and its usage:

What it shows:

The F-table lists critical values for the F-statistic, which is calculated based on the variances in your data. It has two main sections:

  • One-tailed: Used for one-sided tests, where we are interested in the probability of a value falling in one tail of the distribution (e.g., higher than a certain value).
  • Two-tailed: Used for two-sided tests, where we consider both tails of the distribution (e.g., significantly different between groups).

Within each section, you’ll find:

  • Numerator degrees of freedom (df1): Represents the number of groups minus 1 in the numerator of the F-statistic.
  • Denominator degrees of freedom (df2): Represents the total number of observations minus the number of groups in the denominator of the F-statistic.
  • Significance level (α): Represents the probability of rejecting the null hypothesis (H0) when it’s actually true, typically 0.05 (5%) or 0.01 (1%).
  • Critical values: These are specific thresholds for your calculated F-statistic based on df1, df2, and α.

How to use it:

  1. Calculate your F-statistic: This involves using your sample data and the formula for the F-statistic based on the specific F-test you’re conducting (e.g., one-way ANOVA, two-way ANOVA).

  2. Identify the appropriate section: One-tailed for one-sided tests, two-tailed for two-sided tests.

  3. Locate the row with your numerator degrees of freedom (df1).

  4. Find the column with your denominator degrees of freedom (df2).

  5. Compare your calculated F-statistic to the critical value:

    • Reject H0 if your F-statistic is greater than or equal to the critical value. This indicates a statistically significant difference in variances between the groups.
    • Fail to reject H0 if your F-statistic falls below the critical value. This suggests insufficient evidence for a significant difference in variances.

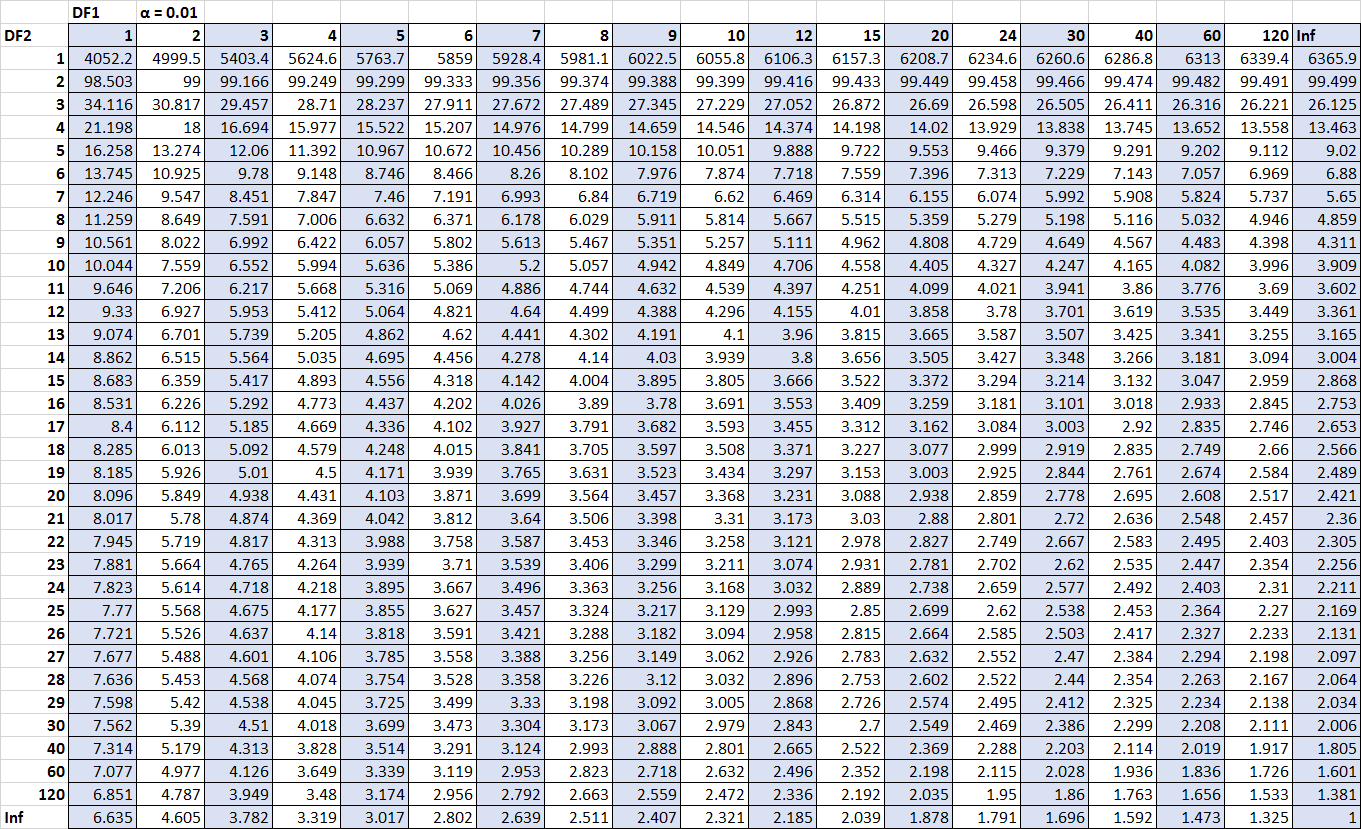
F Table for α = 0.05

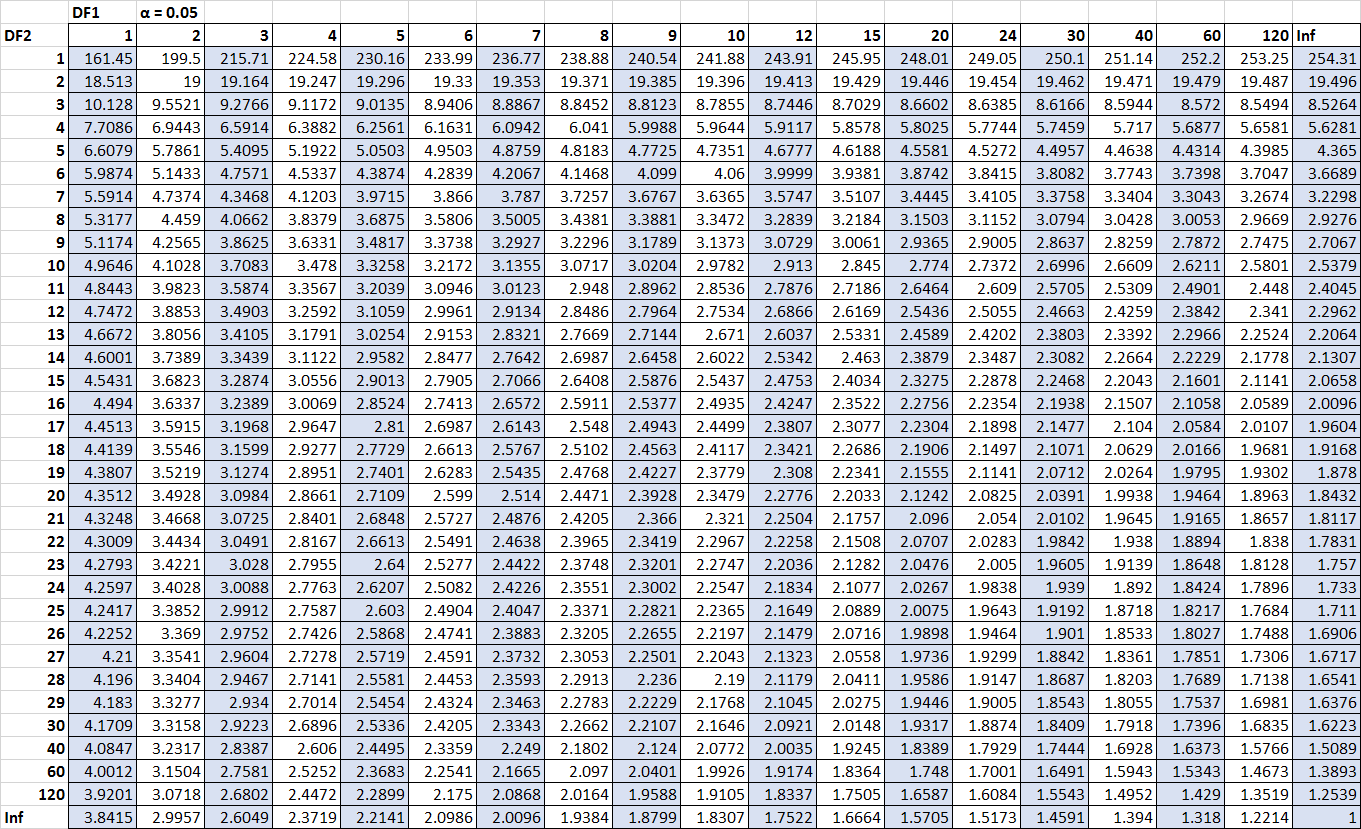
F Table for α = 0.025

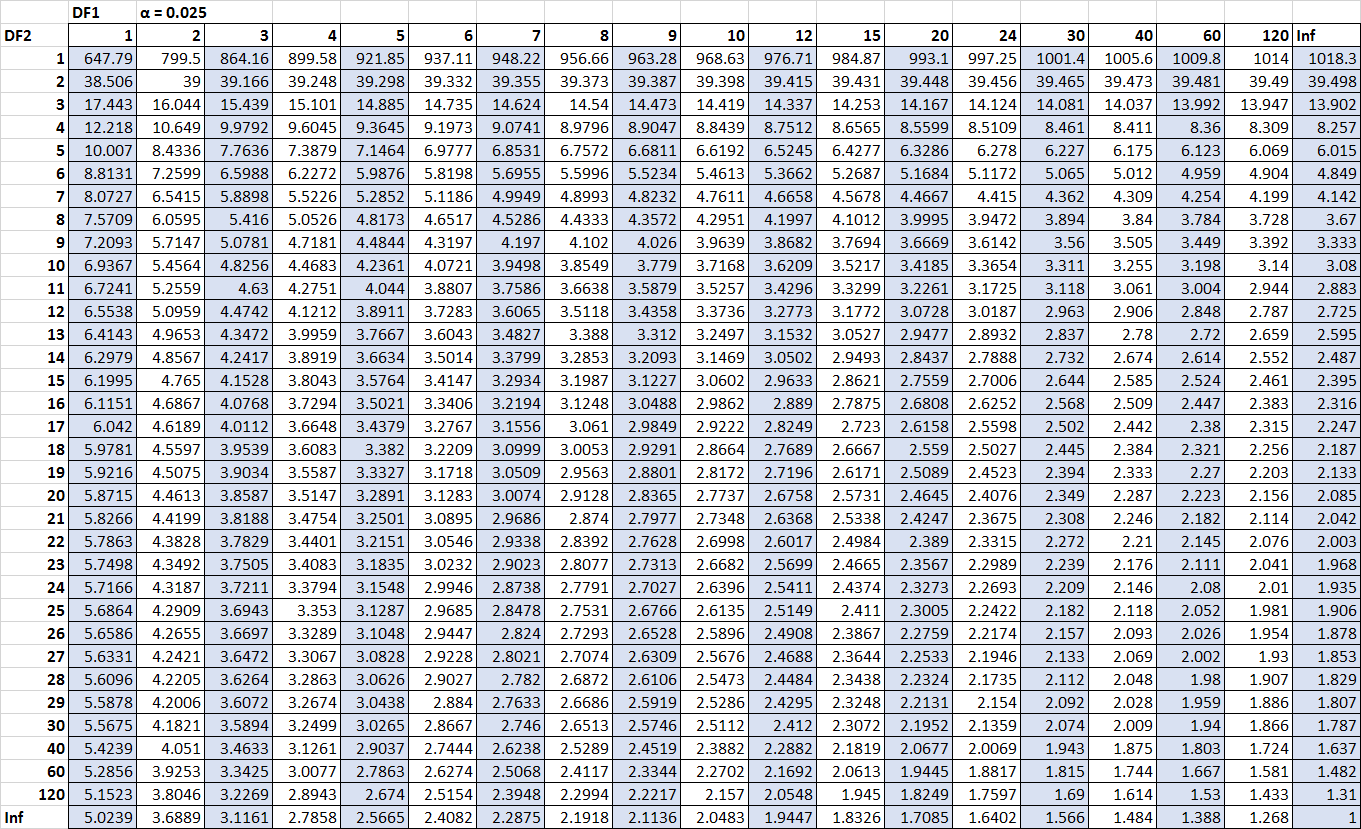
F Table for α = 0.01

x

Related terms:

  1. How to Convert a Pivot Table to a Table in Excel
  2. What is a probability distribution table?
  3. How to read the Binomial Distribution Table
  4. How do you read the Chi-Square Distribution Table?
  5. How do you find the P-Value from the Chi-Square Distribution Table?
  6. Where can I find an F Distribution Table?
  7. What is Chi-square Distribution Table?
  8. t-Distribution Table
  9. Chi-square Distribution Table
  10. Binomial Distribution Table