How to perform a Wilcoxon Signed Rank Test in SAS?

---

The is the non-parametric version of the .

It is used to test whether or not there is a significant difference between two population means when the distribution of the differences between the two samples cannot be assumed to be normal.

The following example shows how to perform a Wilcoxon Signed-Rank Test in SAS.

Example: Wilcoxon Signed-Rank Test in SAS

Suppose an engineer want to know if a new fuel treatment leads to a change in the average miles per gallon of a certain car. To test this, he measures the mpg of 12 cars with and without the fuel treatment.

The results are shown in the table below:

We can use the following code to perform a Wilcoxon Signed-Rank test in SAS to determine if there is a significant difference in the mean mpg between the two groups:

/*create dataset*/
data my_data;
    input car with_fuel without_fuel;
    datalines;
1 20 24
2 23 25
3 21 21
4 25 22
5 18 23
6 17 18
7 18 17
8 24 28
9 20 24
10 24 27
11 23 21
12 19 23
;
run;

/*create new dataset with difference between two fuel treatments*/
data my_data2;
    set my_data;
    diff=with_fuel-without_fuel;
run;

/*perform Wilcoxon Signed Rank Test*/
proc univariate data=my_data2;
    var diff;
run;

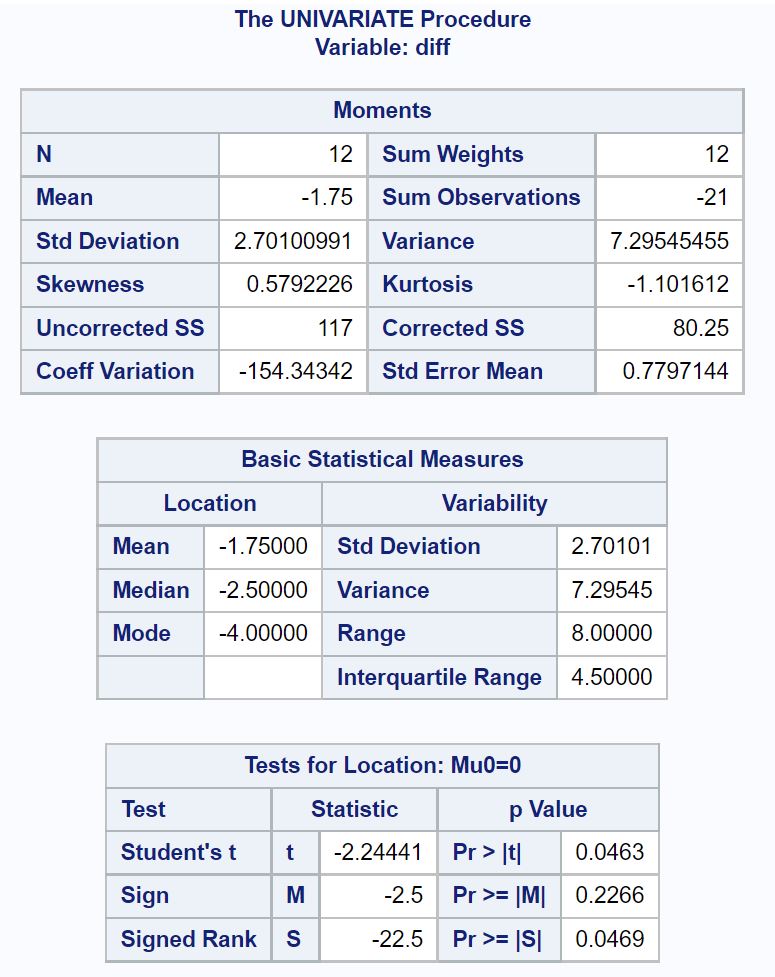
From the output we can see that the mean difference in mpg between the cars that received the treatment and those that didn’t is -1.75.

In the table titled Tests for Location we can observe the following:

• The Wilcoxon Signed-Rank Test statistic: -22.5
• The corresponding p-value: 0.0469

Recall that the Wilcoxon Signed-Rank Test uses the following null and alternative hypotheses:

• H₀: The mpg is equal between the two groups
• H_A: The mpg is not equal between the two groups

Since the of the test (.0469) is less than .05, we reject the null hypothesis.

This means we have sufficient evidence to say that the mean mpg is not equal between the two groups.