Table of Contents
Multinomial Logistic Regression is a statistical method used for predicting categorical outcomes with three or more categories. It is an extension of binary logistic regression, which is used for predicting binary outcomes. This method models the relationship between a set of independent variables and a dependent variable with multiple categories, by estimating the probability of each category. It is commonly used in fields such as economics, marketing, and social sciences, where the outcome of interest has more than two possible outcomes. Multinomial Logistic Regression is a powerful tool for analyzing and predicting complex categorical data.
What is Multinomial Logistic Regression?
Multinomial Logistic Regression is a statistical test used to predict a single categorical variable using one or more other variables. It also is used to determine the numerical relationship between such sets of variables. The variable you want to predict should be categorical and your data should meet the other assumptions listed below.
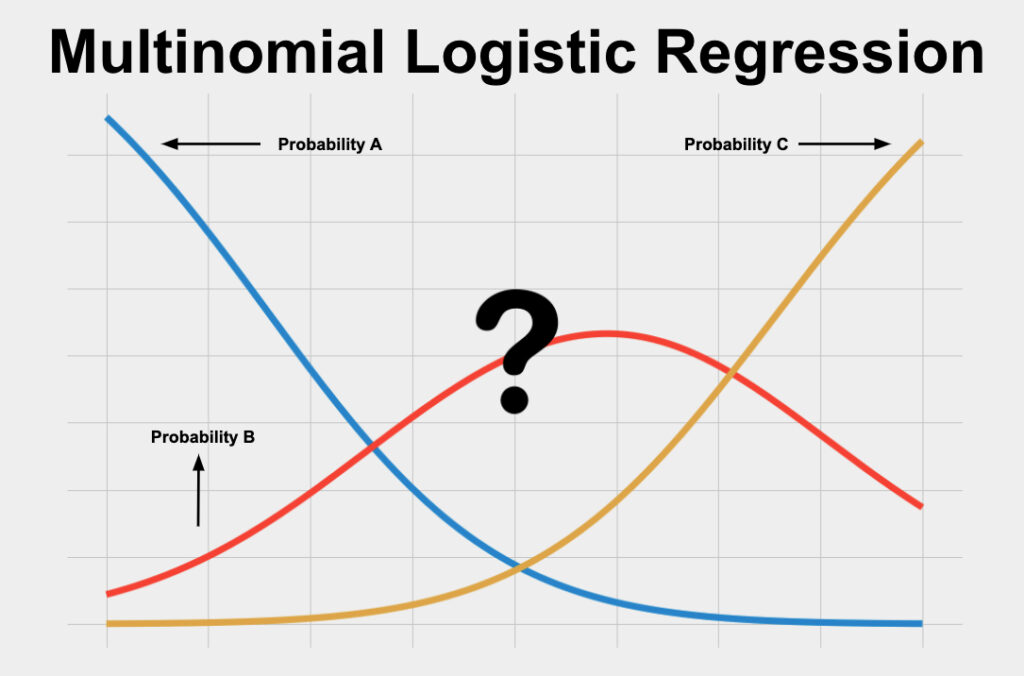
Multinomial Logistic Regression is sometimes also called multi-class logistic regression, and multinomial logit (mlogit).
Assumptions for Multinomial Logistic Regression
Every statistical method has assumptions. Assumptions mean that your data must satisfy certain properties in order for statistical method results to be accurate.
The assumptions for Multinomial Logistic Regression include:
- Linearity
- No Outliers
- Independence
- No Multicollinearity
Let’s dive in to each one of these separately.
Linearity
Logistic regression fits a logistic curve to binary data. This logistic curve can be interpreted as the probability associated with each outcome across independent variable values. Logistic regression assumes that the relationship between the natural log of these probabilities (when expressed as odds) and your predictor variable is linear.
No Outliers
The variables that you care about must not contain outliers. Logistic Regression is sensitive to outliers, or data points that have unusually large or small values. You can tell if your variables have outliers by plotting them and observing if any points are far from all other points.
Independence
Each of your observations (data points) should be independent. This means that each value of your variables doesn’t “depend” on any of the others. For example, this assumption is usually violated when there are multiple data points over time from the same unit of observation (e.g. subject/participant/customer/store), because the data points from the same unit of observation are likely to be related or affect one another.
No Multicollinearity
Multicollinearity refers to the scenario when two or more of the independent variables are substantially correlated amongst each other. When multicollinearity is present, the regression coefficients and statistical significance become unstable and less trustworthy, though it doesn’t affect how well the model fits the data per se.
When to use Multinomial Logistic Regression?
You should use Multinomial Logistic Regression in the following scenario:
- You want to use one variable in a prediction of another, or you want to quantify the numerical relationship between two variables
- The variable you want to predict (your dependent variable) is categorical
- Your dependent variables are not all continuous
Let’s clarify these to help you know when to use Multinomial Logistic Regression
Prediction
You are looking for a statistical test to predict one variable using another. This is a prediction question. Other types of analyses include examining the strength of the relationship between two variables (correlation) or examining differences between groups (difference).
Categorical Dependent Variable
A categorical variable is a variable that describes a category that doesn’t relate naturally to a number. Examples of categorical variables are eye color, city of residence, type of dog, etc..
Types of data that are NOT categorical include ordered data (such as finishing place in a race, best business rankings, etc.), binary data (true/false, purchased the product or not, etc.), or continuous data (height, income, etc.).
If your dependent variable is continuous, you should use Simple Linear Regression, and if your dependent variable is binary, then you should use Simple Logistic Regression.
Not All Continuous
Multinomial Logistic Regression is a method that can be used when one or more of the predictor variables are not continuous in addition to when they are continuous.
If your independent variables are all continuous, then you can also use Linear Discriminant Analysis.
Multinomial Logistic Regression Example
Dependent Variable: Website format preference (e.g. format A, B, C, etc)
Independent Variable: Consumer income
The null hypothesis, which is statistical lingo for what would happen if the treatment does nothing, is that there is no relationship between consumer income and consumer website format preference. Our test will assess the likelihood of this hypothesis being true.
We gather our data and after assuring that the assumptions of multinomial logistic regression are met, we perform the analysis.
When we run this analysis, we get coefficients for each term in the model. These coefficients can be used to determine the predicted numerical relationship between consumer income and the probability of each consumer preferring a particular website format.
Each model coefficient also has an associated P-value. These p-values represent the chance of seeing our results assuming there is actually no relationship between consumer income and website format preference. A p-value less than or equal to 0.05 means that our result is statistically significant and we can trust that the difference is not due to chance alone.
