One-Way ANCOVA

---

What is a One-Way ANCOVA?

The One-Way ANCOVA is a statistical test used to determine if 3 or more groups are significantly different from each other on your variable of interest while accounting for the effect of another variable (called a covariate). Your variable of interest should be continuous, be normally distributed, and have a similar spread across your groups. Your groups should be independent (not related to each other) and you should have enough data (more than 5 values in each group).

The One-Way ANCOVA is also sometimes called Analysis of Covariance, One-Way Analysis of Covariance and the One-Way ANCOVA F-Test

---

Assumptions for the One-Way ANCOVA

Every statistical method has assumptions. Assumptions mean that your data must satisfy certain properties in order for statistical method results to be accurate.

The assumptions for the One-Way ANCOVA include:

1. Continuous
2. Normally Distributed
3. Random Sample
4. Enough Data
5. Similar Spread Across Groups

Let’s dive in to each one of these separately.

Continuous

The variable that you care about (and want to see if it is different across the 3+ groups) must be continuous. Continuous means that the variable can take on any reasonable value.

Some good examples of continuous variables include age, weight, height, test scores, survey scores, yearly salary, etc.

Normally Distributed

The variable that you care about must be spread out in a normal way. In statistics, this is called being normally distributed (aka it must look like a bell curve when you graph the data). Only use a One-Way ANCOVA with your data if the variable you care about is normally distributed.

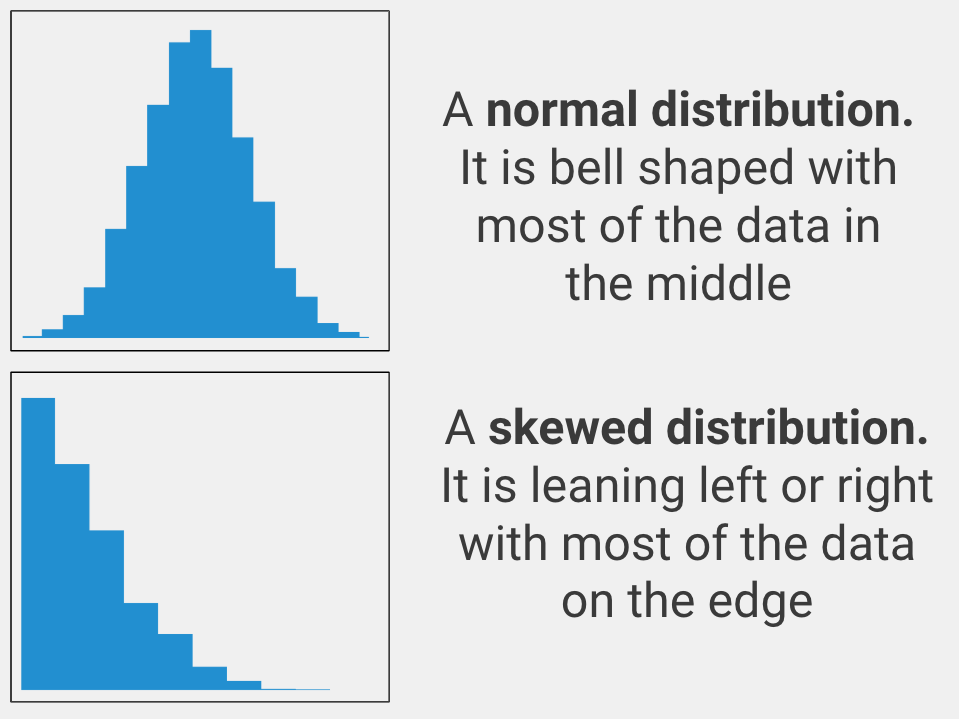
If your variable is not normally distributed, you should use the Kruskal-Wallis One-Way ANOVA instead.

Random Sample

The data points for each group in your analysis must have come from a simple random sample. This means that if you wanted to see if drinking sugary soda makes you gain weight, you would need to randomly select a group of soda drinkers for your soda drinker group.

The key here is that the data points for each group were randomly selected. This is important because if your groups were not randomly determined then your analysis will be incorrect. In statistical terms this is called bias, or a tendency to have incorrect results because of bad data.

If you do not have a random sample, the conclusions you can draw from your results are very limited. You should try to get a simple random sample.If you have paired samples (2 or more measurements from the same groups of subjects) then you should use a One-Way Repeated Measures ANOVA instead.

Enough Data

The sample size (or data set size) should be greater than 5 in each group. Some people argue for more, but more than 5 is probably sufficient.

The sample size also depends on the expected size of the difference across groups. If you expect a large difference across groups, then you can get away with a smaller sample size. If you expect a small difference across groups, then you likely need a larger sample.

Similar Spread Across Groups

In statistics this is called homogeneity of variance, or making sure the variables take on reasonably similar values. To examine this assumption, you can plot your data as in the figure below and see if the groups are similarly spread on your variable of interest.

---

When to use a One-Way ANCOVA?

You should use a One-Way ANCOVA in the following scenario:

1. You want to know if many groups are different on your variable of interest
2. Your variable of interest is continuous
3. You have 3 or more groups
4. You have independent samples
5. You have a normal variable of interest
6. You want to account for the effects of another variable (you have a covariate)

Let’s clarify these to help you know when to use a One-Way ANCOVA.

Difference

You are looking for a statistical test to see whether two groups are significantly different on your variable of interest. This is a difference question. Other types of analyses include examining the relationship between two variables (correlation) or predicting one variable using another variable (prediction).

Continuous Data

Your variable of interest must be continuous. Continuous means that your variable of interest can basically take on any value, such as heart rate, height, weight, number of ice cream bars you can eat in 1 minute, etc.

Types of data that are NOT continuous include ordered data (such as finishing place in a race, best business rankings, etc.), categorical data (gender, eye color, race, etc.), or binary data (purchased the product or not, has the disease or not, etc.).

Three or more Groups

A One-Way ANCOVA can be used to compare three or more groups on your variable of interest.

If you have only two groups and don’t have a covariate, you should use an Independent Samples T-Test instead. If you want to compare two groups with a covariate, you might want to use Multiple Linear Regression. If you only have one group and you would like to compare your group to a known or hypothesized population value, you should use a Single Sample T-Test instead.

Independent Samples

Independent samples means that your groups are not related in any way. For example, if you randomly sample men and then separately randomly sample women to get their heights, the groups should not be related.

If you get multiple groups of students to take a pre-test and those same students to take a post-test, you have two different variables for the same groups of students, which would be paired data, in which case you would need to use a One-Way Repeated Measures ANOVA instead.

Normal Variable of Interest

Normality was discussed earlier on this page and simply means your plotted data is bell shaped with most of the data in the middle. If you actually would like to prove that your data is normal, you can use the Kolmogorov-Smirnov test or the Shapiro-Wilk test.

Covariate

A covariate is a variable you want to account for when examining the difference across your groups on your variable of interest.

For example, a study on the effect of different types of exercise routines on cardiovascular endurance could potentially be confounded by the subjects initial level of endurance. The hypothesis might be that people with higher endurance to begin with don’t have as much room for growth compared to those with low initial endurance and so wouldn’t be as responsive to any exercise routine. Adding initial endurance as a covariate accounts for this effect.

---

One-Way ANCOVA Example

Group 1: Received medical treatment #1.
Group 2: Received medical treatment #2.
Group 3: Received a placebo or control condition.
Covariate: Body Weight
Variable of interest: Time in days to recover from a disease.

In this example we have three independent groups and one continuous variable of interest. Since we think that body weight might account for some differences in time to recover, we add it to the analysis as a covariate. After confirming that our variable of interest is normal and our data meet the other assumptions of One-Way ANCOVA, we proceed with the analysis.

The null hypothesis, which is statistical lingo for what would happen if the treatments do nothing, is that none of the three groups have different recovery times on average after accounting for the effect of body weight. We are trying to determine if receiving either of the medical treatments will shorten the number of days it takes for patients to recover from the disease.

After the experiment is over, we compare the three groups on our variable of interest (days to fully recover) using a One-Way ANCOVA. When we run the analysis, we get an F-statistic and a p-value. The F-statistic is a measure of how different the three groups are on our recovery variable of interest after accounting for body weight.

A p-value is the chance of seeing our results assuming neither of the treatments actually change recovery time. A p-value less than or equal to 0.05 means that our result is statistically significant and we can trust that the difference is not due to chance alone.

If the F-statistic is high and the p-value is low, it means that the recovery time was significantly different in at least one of the groups. Further investigation is required to determine the which group(s) was significantly higher/lower than the others.