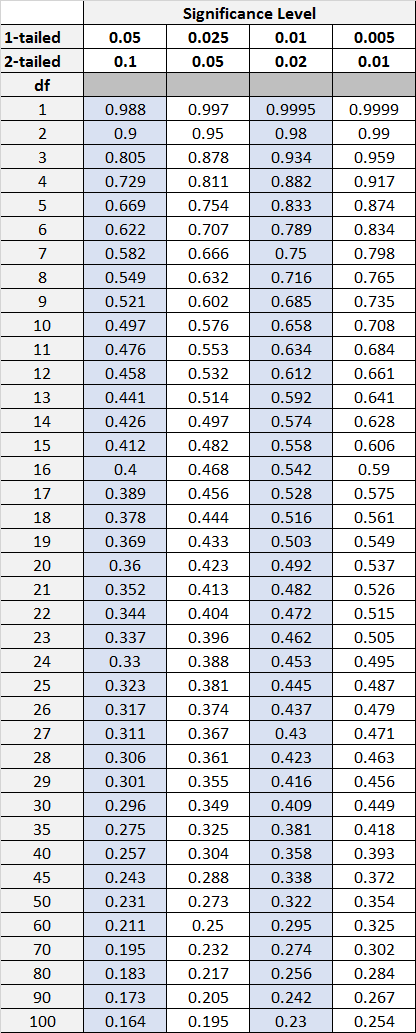
The Pearson Correlation Table, also known as the “Critical Values Table for Pearson’s r,” is a helpful tool in statistics for interpreting the results of the Pearson correlation coefficient. Here’s a breakdown of the table and its significance:
What it provides:
- This table presents critical values for the Pearson correlation coefficient (r) based on two factors:
- Sample size (n): The number of pairs of data points you analyzed.
- Significance level (α): The probability of rejecting the null hypothesis (H0) when it’s actually true, typically set at 0.05 (5%) or 0.01 (1%).
How to use it:
-
Calculate your Pearson correlation coefficient (r): This statistic measures the strength and direction of the linear relationship between two variables.
-
Look up the critical value based on your sample size (n) and chosen significance level (α): Each combination of n and α has a corresponding critical value in the table.
-
Compare your calculated r to the critical value:
- Two-tailed test: If your r is greater than or equal to the critical value in absolute value, reject the null hypothesis (H0) and conclude that there is a significant correlation between the variables.
- One-tailed test: Double your chosen α and use the table accordingly. Reject H0 if r is greater than or equal to (for positive correlation) or less than or equal to (for negative correlation) the adjusted critical value.
Interpreting the results:
- The closer your calculated r is to 1 or -1, the stronger the positive or negative correlation, respectively.
- A non-significant result (r falls within the range defined by the critical values) doesn’t necessarily mean no correlation exists, but that the evidence in your sample isn’t strong enough to claim one statistically.