How to calculate correlation between multiple variables in R?

---

One way to quantify the relationship between two variables is to use the Pearson correlation coefficient, which is a measure of the linear association between two variables. It always takes on a value between -1 and 1 where:

• -1 indicates a perfectly negative linear correlation between two variables
• 0 indicates no linear correlation between two variables
• 1 indicates a perfectly positive linear correlation between two variables

This tutorial explains how to calculate the correlation between multiple variables in R, using the following data frame as an example:

#create data frame
df <- data.frame(a <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23),
                 b <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43),
                 c <- c(13, 14, 14, 14, 15, 17, 18, 19, 22, 20, 24, 26),
                 d <- c(6, 6, 7, 8, 8, 8, 7, 6, 5, 3, 3, 2))

Example 1: Correlation Between Two Variables

The following code shows how to calculate the correlation between two variables in the data frame:

cor(df$a, df$b)

[1] 0.9279869

Example 2: Correlation Between Multiple Variables

The following code shows how to calculate the correlation between three variables in the data frame:

cor(df[, c('a', 'b', 'c')])

          a         b         c
a 1.0000000 0.9279869 0.9604329
b 0.9279869 1.0000000 0.8942139
c 0.9604329 0.8942139 1.0000000

The way to interpret the output is as follows:

• The correlation between a and b is 0.9279869.
• The correlation between a and c is 0.9604329.
• The correlation between b and c is 0.8942139.

Example 3: Correlation Between All Variables

The following code shows how to calculate the correlation between all variables in a data frame:

cor(df)

           a          b          c          d
a  1.0000000  0.9279869  0.9604329 -0.7915488
b  0.9279869  1.0000000  0.8942139 -0.7917973
c  0.9604329  0.8942139  1.0000000 -0.8063549
d -0.7915488 -0.7917973 -0.8063549  1.0000000

Example 4: Correlation Between Only Numerical Variables

The following code shows how to calculate the correlation between only the numerical variables in a data frame:

cor(df[,unlist(lapply(df, is.numeric))])

           a          b          c          d
a  1.0000000  0.9279869  0.9604329 -0.7915488
b  0.9279869  1.0000000  0.8942139 -0.7917973
c  0.9604329  0.8942139  1.0000000 -0.8063549
d -0.7915488 -0.7917973 -0.8063549  1.0000000

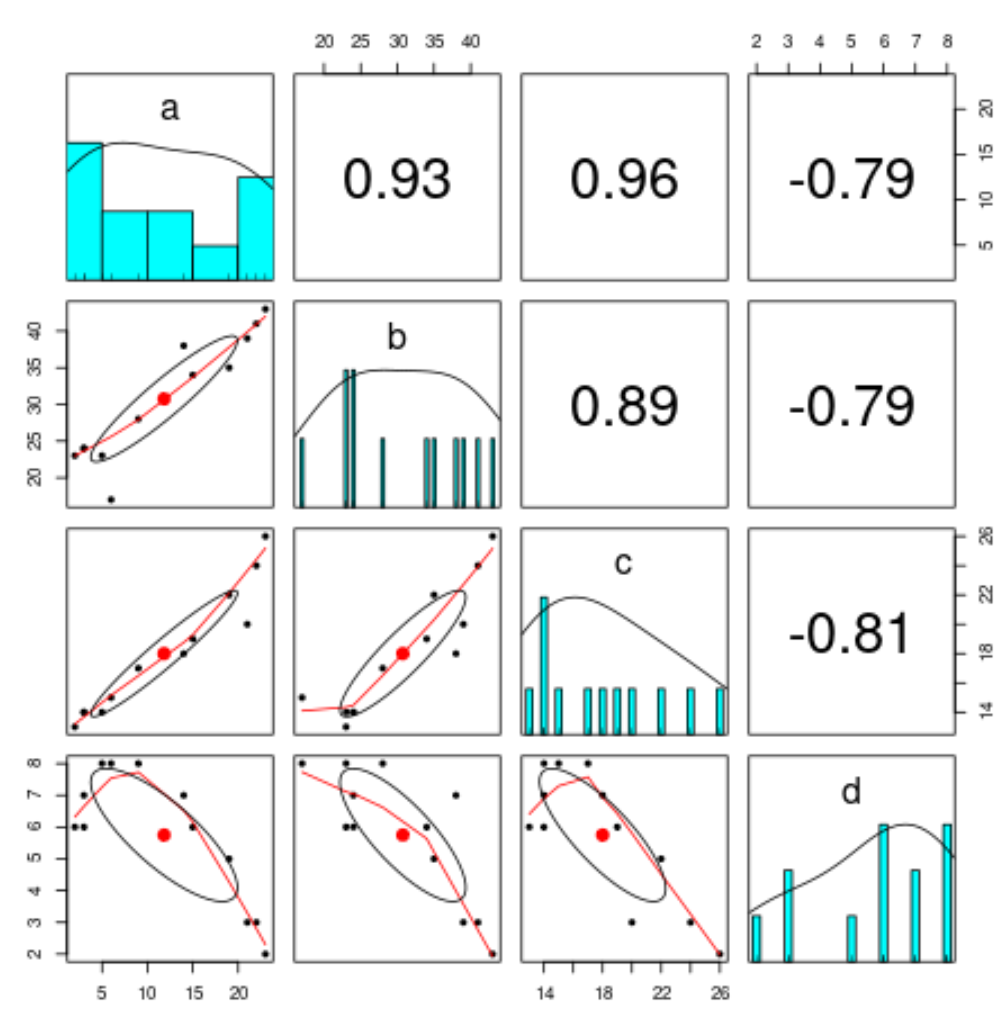
Example 5: Visualize Correlations

The following code shows how to create a pairs plot – a type of plot that lets you visualize the relationship between each pairwise combination of variables:

#load psych package
library(psych)

#create pairs plot
pairs.panels(df)