What are the Five Assumptions for Pearson Correlation?

---

The Pearson correlation coefficient (also known as the “product-moment correlation coefficient”) measures the linear association between two variables.

It always takes on a value between -1 and 1 where:

• -1 indicates a perfectly negative linear correlation between two variables
• 0 indicates no linear correlation between two variables
• 1 indicates a perfectly positive linear correlation between two variables

However, before we calculate the Pearson correlation coefficient between two variables we should make sure that five assumptions are met:

1. Level of Measurement: The two variables should be measured at the interval or ratio level.

2. Linear Relationship: There should exist a linear relationship between the two variables.

3. Normality: Both variables should be roughly normally distributed.

4. Related Pairs: Each observation in the dataset should have a pair of values.

5. No Outliers: There should be no extreme outliers in the dataset.

In this article, we provide an explanation for each assumption along with how to determine if the assumption is met.

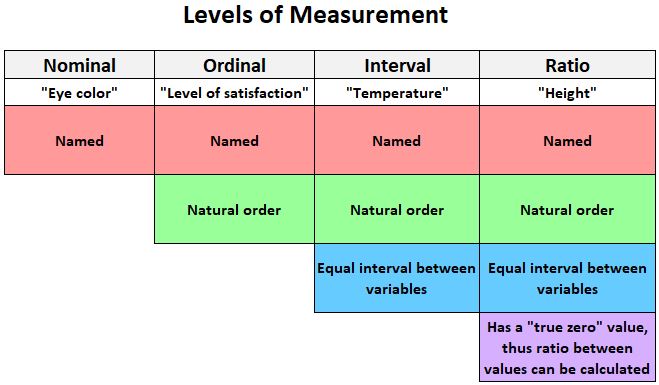
Assumption 1: Level of Measurement

To calculate a Pearson correlation coefficient between two variables, both of the variables should be measured at the interval or ratio level.

The following graphic provides a quick explanation of the four levels that variables can be measured at:

Some examples of variables that can be measured on an interval scale include:

• Temperature: Measured in Fahrenheit or Celsius
• Credit Scores: Measured from 300 to 850
• SAT Scores: Measured from 400 to 1,600

Some examples of variables that can be measured on a ratio scale include:

• Height: Measured in centimeters, inches, feet, etc.
• Weight: Measured in kilograms, pounds, etc.
• Length: Measured in centimeters, inches, feet, etc.

If the variables are measured at an ordinal level, then you should instead calculate the between them.

Related:

Assumption 2: Linear Relationship

To calculate a Pearson Correlation coefficient between two variables, there should exist a linear relationship between the two variables.

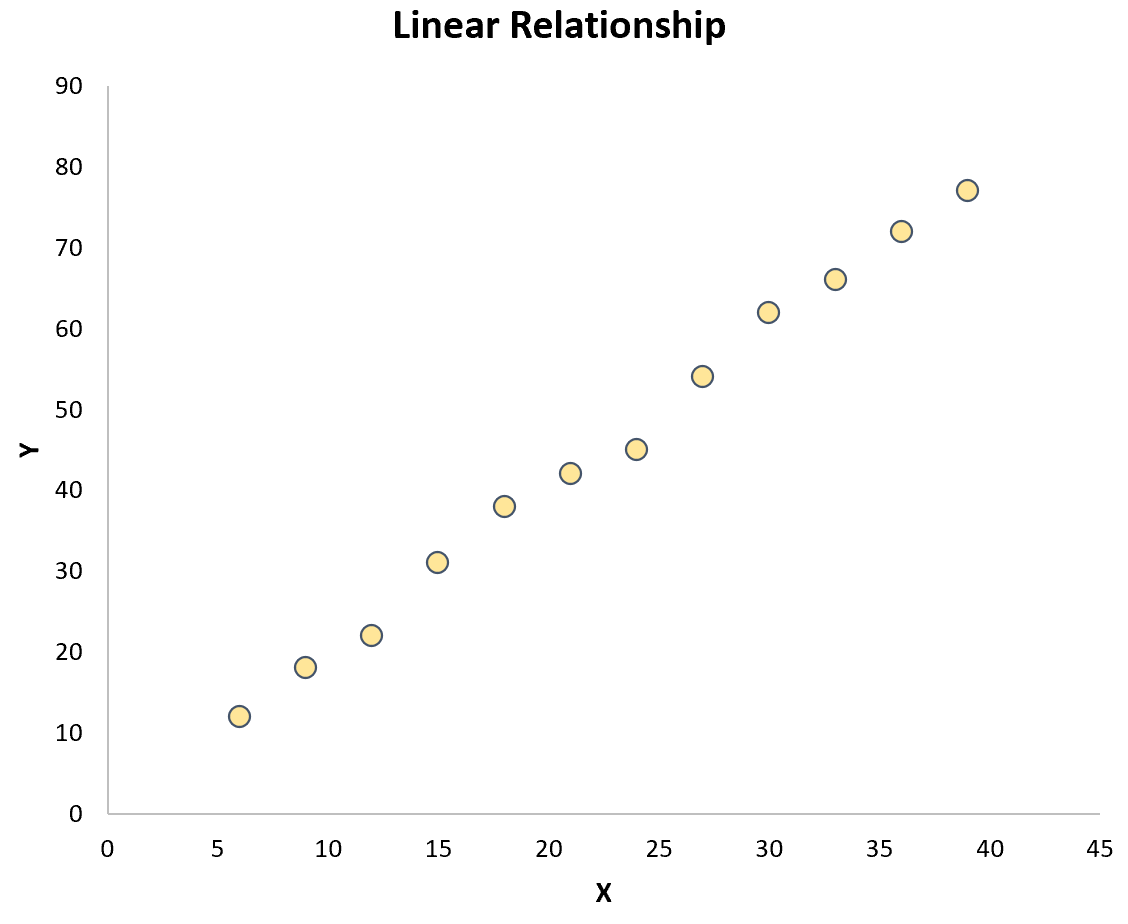
The easiest way to check this assumption is to simply create a scatter plot of the two variables. If the points in the plot fall roughly along a straight line, then a linear relationship exists:

However, if the points are randomly scattered about the plot or if they exhibit some other type of relationship (like quadratic) then a linear relationship does not exist between the variables:

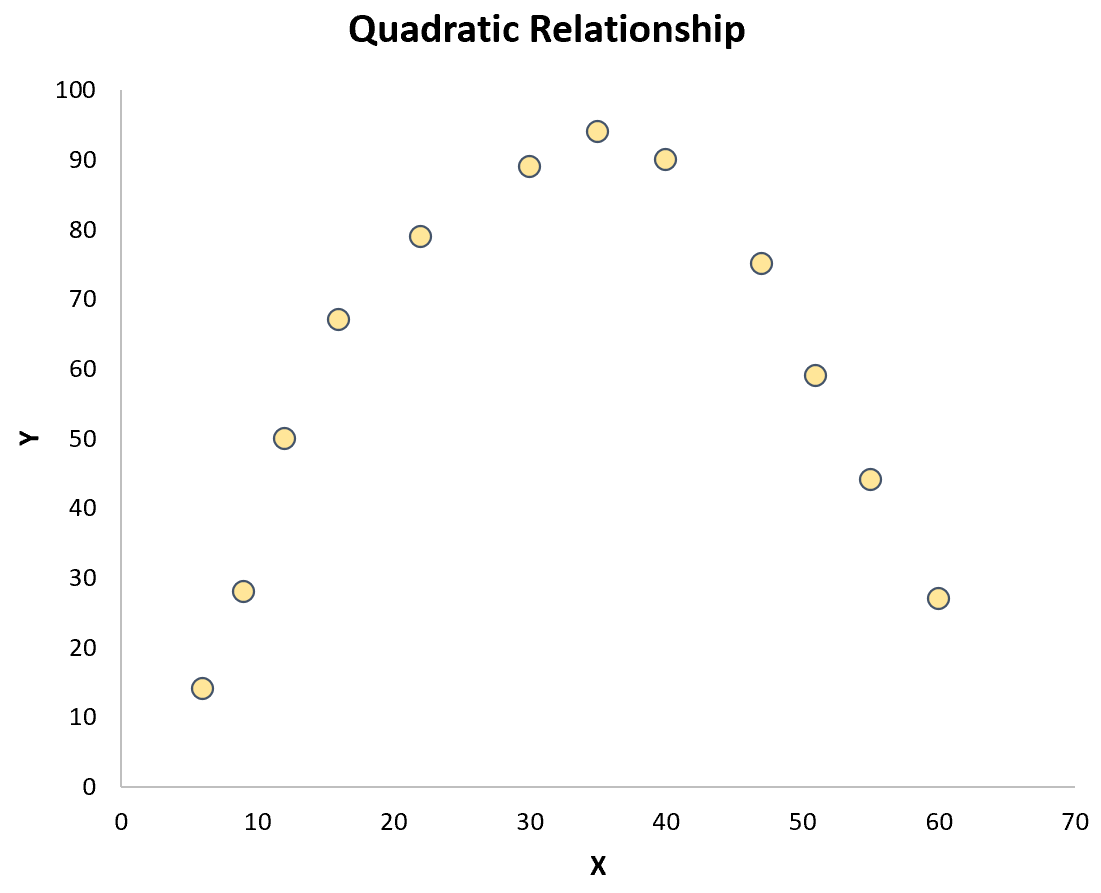
In this case, a Pearson Correlation coefficient won’t do a good job of capturing the relationship between the variables.

Assumption 3: Normality

A Pearson Correlation coefficient also assumes that both variables are roughly .

You can check this assumption visually by creating a histogram or a Q-Q plot for each variable.

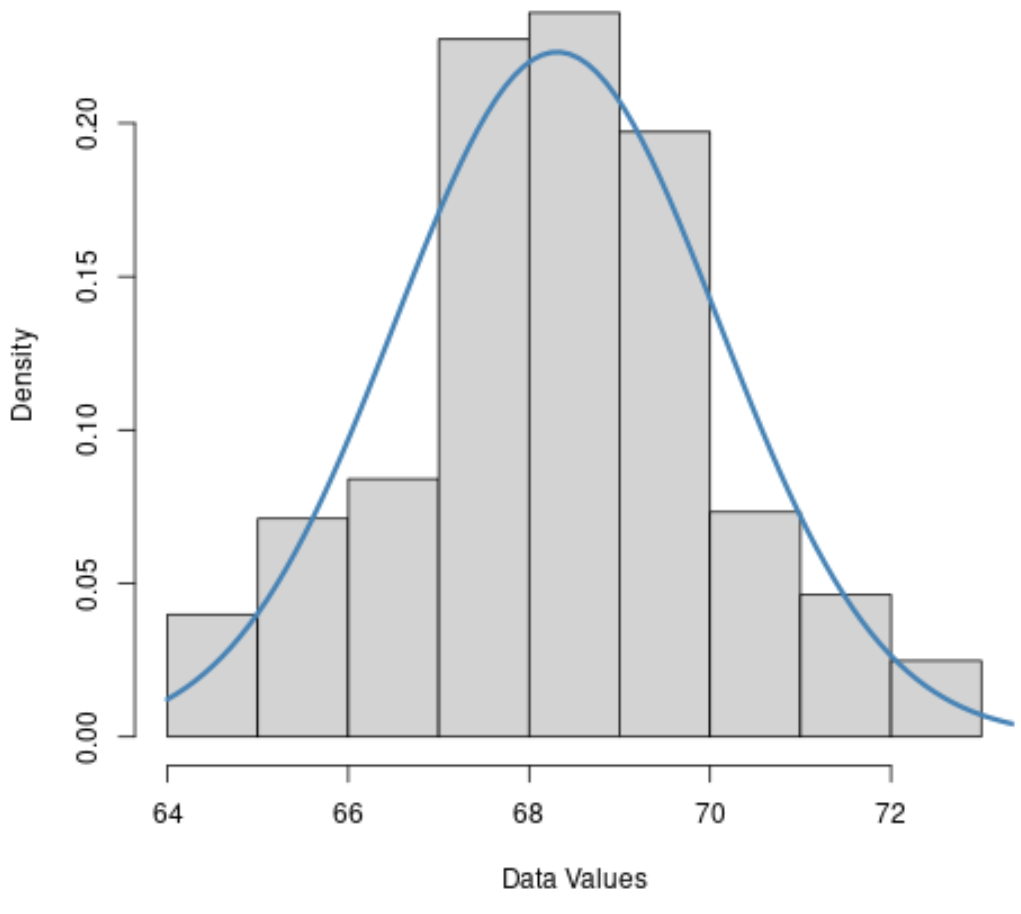
1. Histogram

If a histogram for a dataset is roughly bell-shaped, then it’s likely that the data is normally distributed.

2. Q-Q Plot

A Q-Q plot, short for “quantile-quantile” plot, is a type of plot that displays theoretical quantiles along the x-axis (i.e. where your data would lie if it did follow a normal distribution) and sample quantiles along the y-axis (i.e. where your data actually lies).

If the data values fall along a roughly straight line at a 45-degree angle, then the data is assumed to be normally distributed.

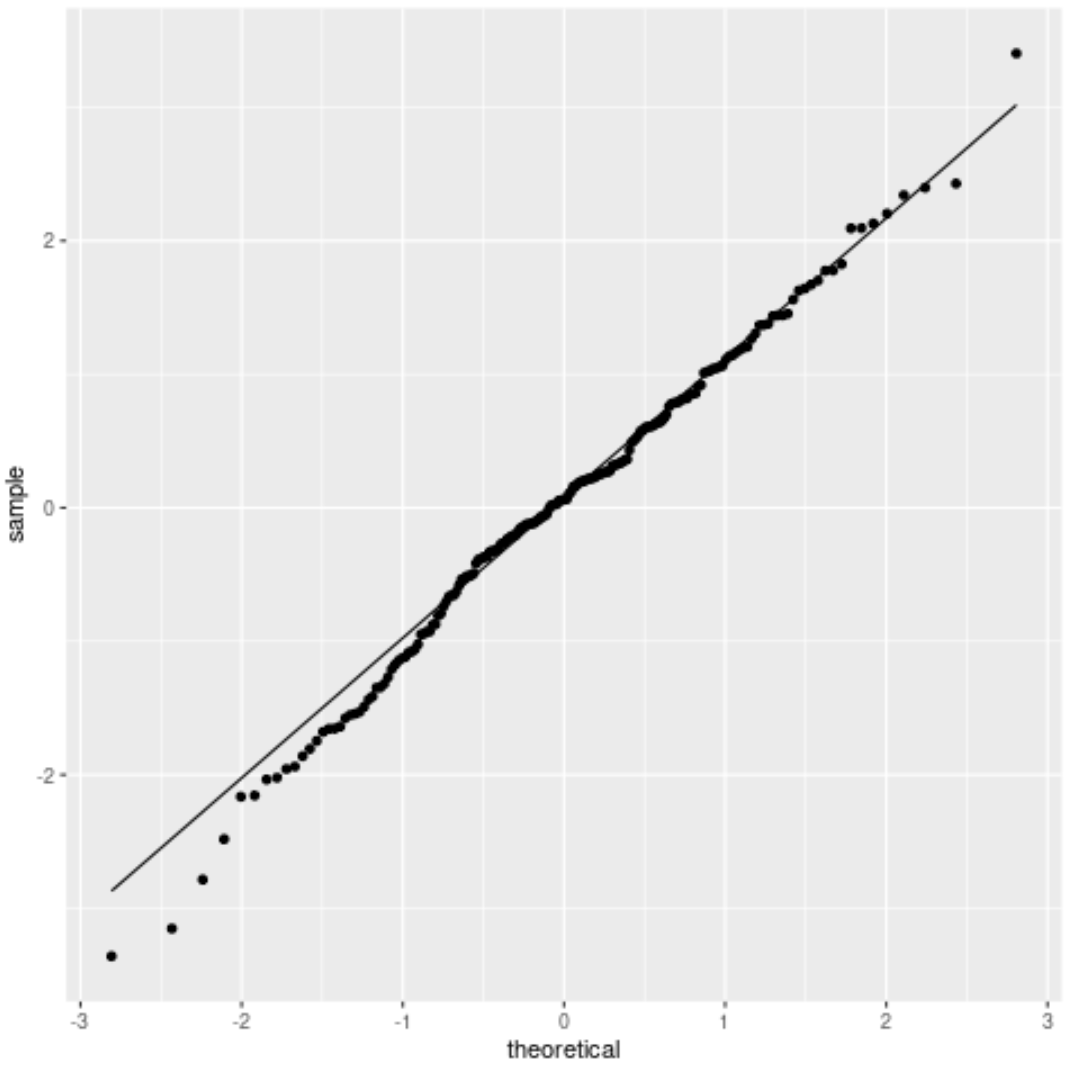
You can also perform a formal statistical test to determine if a variable is normally distributed.

If the of the test is less than a certain significance level (like α = 0.05) then you have sufficient evidence to say that the data is not normally distributed.

There are three statistical tests that are commonly used to test for normality:

1. The Jarque-Bera Test

2. The Shapiro-Wilk Test

3. The Kolmogorov-Smirnov Test

Assumption 4: Related Pairs

A Pearson Correlation coefficient also assumes that each in the dataset should have a pair of values.

This assumption is easy to check. For example, if you’re calculating the correlation between weight and height then simply verify that each observation in the dataset has one measurement for weight and one measurement for height.

Assumption 5: No Outliers

A Pearson Correlation coefficient also assumes that there are no extreme outliers in the dataset since outliers heavily affect the calculation of the correlation coefficient.

To illustrate this, consider the following dataset:

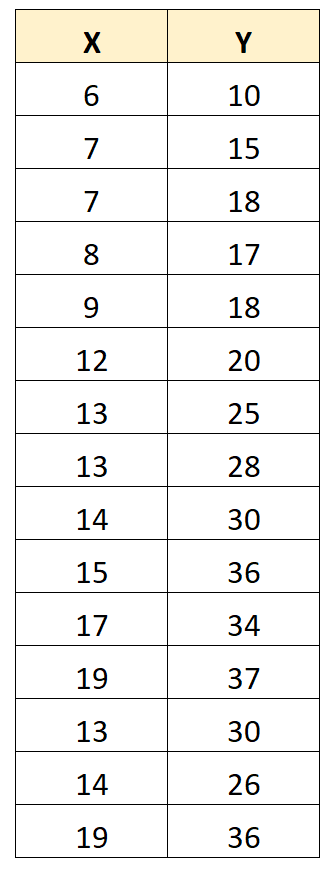
The Pearson Correlation coefficient between X and Y is 0.949.

However, suppose we have one outlier in the dataset:

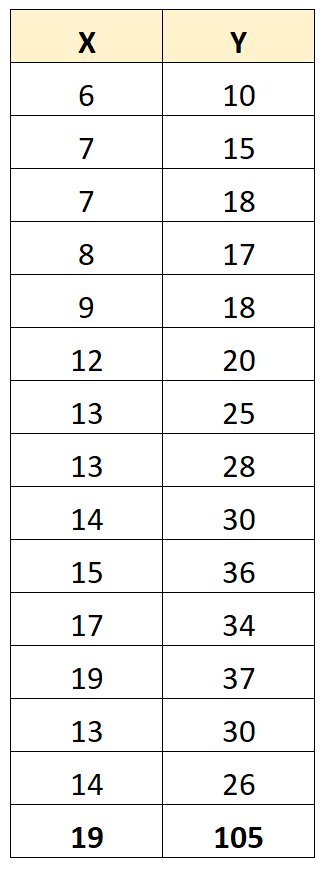
The Pearson Correlation coefficient between X and Y is now 0.711.

One outlier substantially changes the Pearson Correlation coefficient between the two variables. In this case, it could make sense to remove the outlier from the dataset.

Related:

The following tutorials provide additional information about Pearson correlation: