Table of Contents

No, causation does not imply correlation. For example, a person’s age is not necessarily correlated to their intelligence, but it does cause them to have more life experience. Similarly, a person’s nationality is not necessarily correlated to their income, but it does cause them to have access to certain economic opportunities. Finally, a person’s gender is not necessarily correlated to their job performance, but it may cause them to have different expectations or experiences in the workplace.

It’s well-known that .

As a simple example, if we collect data for the total number of high school graduates and total pizza consumption in the U.S. each year, we would find that the two variables are highly correlated:

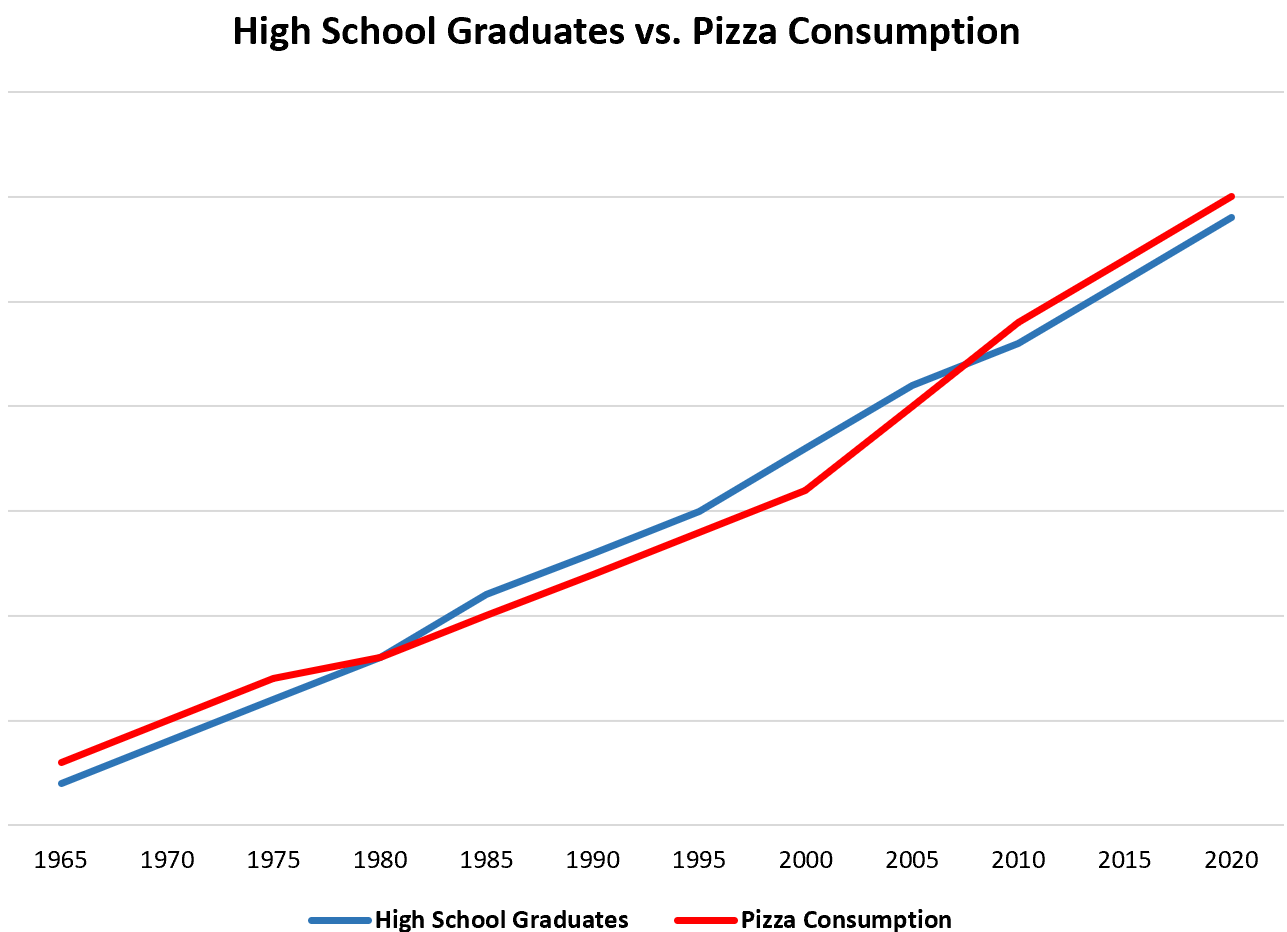
This doesn’t mean that an increased number of high school graduates is causing more pizza consumption.

The more likely explanation is that U.S. population has been increasing over time, which means that the number of people receiving a high school degree and the total pizza being consumed are both increasing as population increases.

But what about the reverse statement: Does causation imply correlation?

If one variable causes another variable, does it necessarily mean that the two variables will be correlated?

The short answer: No.

The following examples show why.

Example 1: Quadratic Relationship

Suppose some variable, X, causes variable Y to take on a value equal to X².

For example:

If X = -10 then Y = -10² = 100
If X = 0 then Y = 0² = 0
If X = 10 then Y = 10² = 100

And so on.

If we plotted the relationship between X and Y, it would look like this:

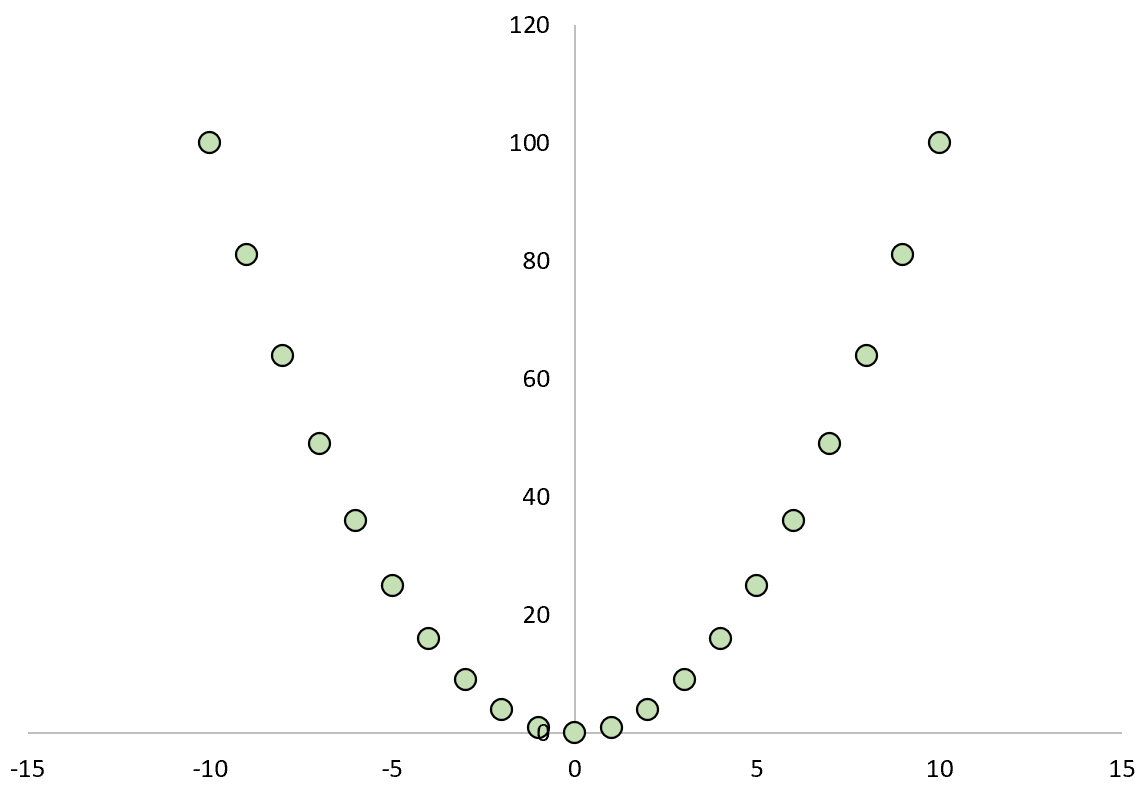
If we calculated the between the two variables, we would find that the correlation is zero.

Example 2: Quartic Relationship

Suppose some variable, X, causes variable Y to take on a value equal to X⁴.

For example:

If X = -10 then Y = -10⁴ = 10,000
If X = 0 then Y = 0⁴ = 0
If X = 10 then Y = 10⁴ = 10,000

And so on.

If we plotted the relationship between X and Y, it would look like this:

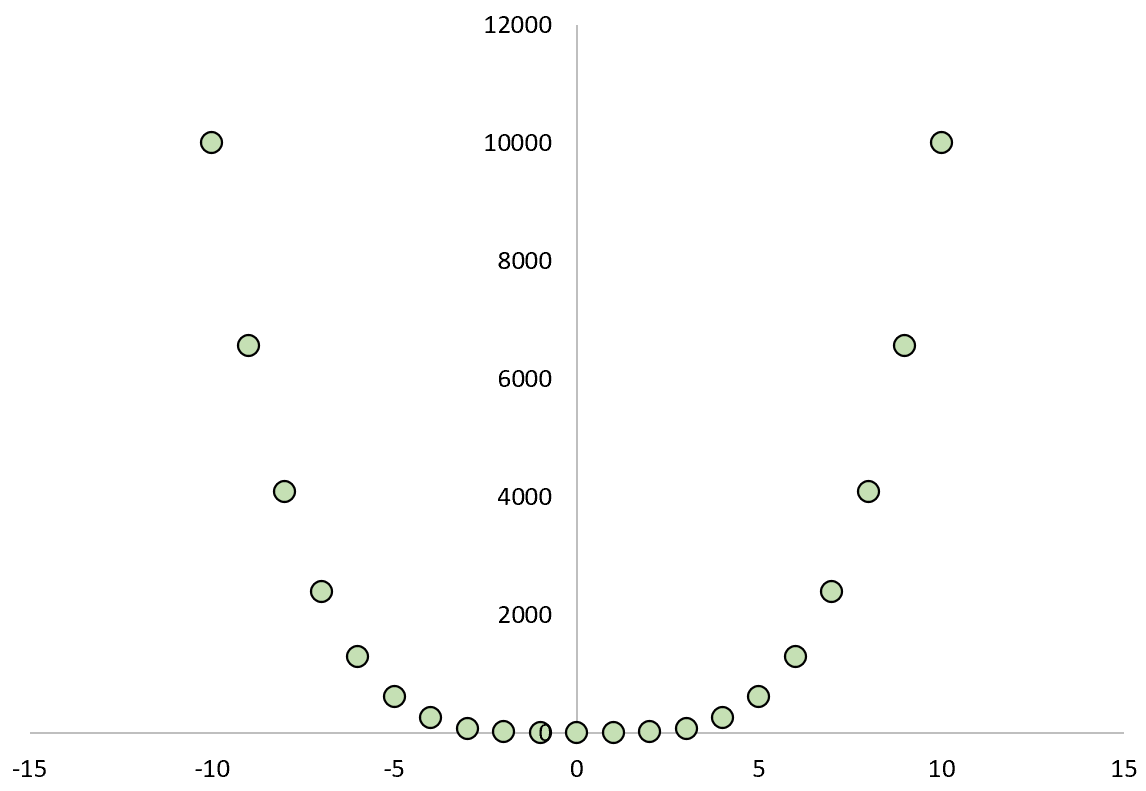
If we calculated the between the two variables, we would find that the correlation is zero.

We know that X causes Y, but the linear correlation between the two variables is zero.

Example 3: Cosine Relationship

Suppose some variable, X, causes variable Y to take on a value equal to cos(X).

For example:

If X = -10 then Y = cos(-10) = -0.83907
If X = 0 then Y = cos(0) = 1
If X = 10 then Y = cos(10) = -0.83907

And so on.

If we plotted the relationship between X and Y, it would look like this:

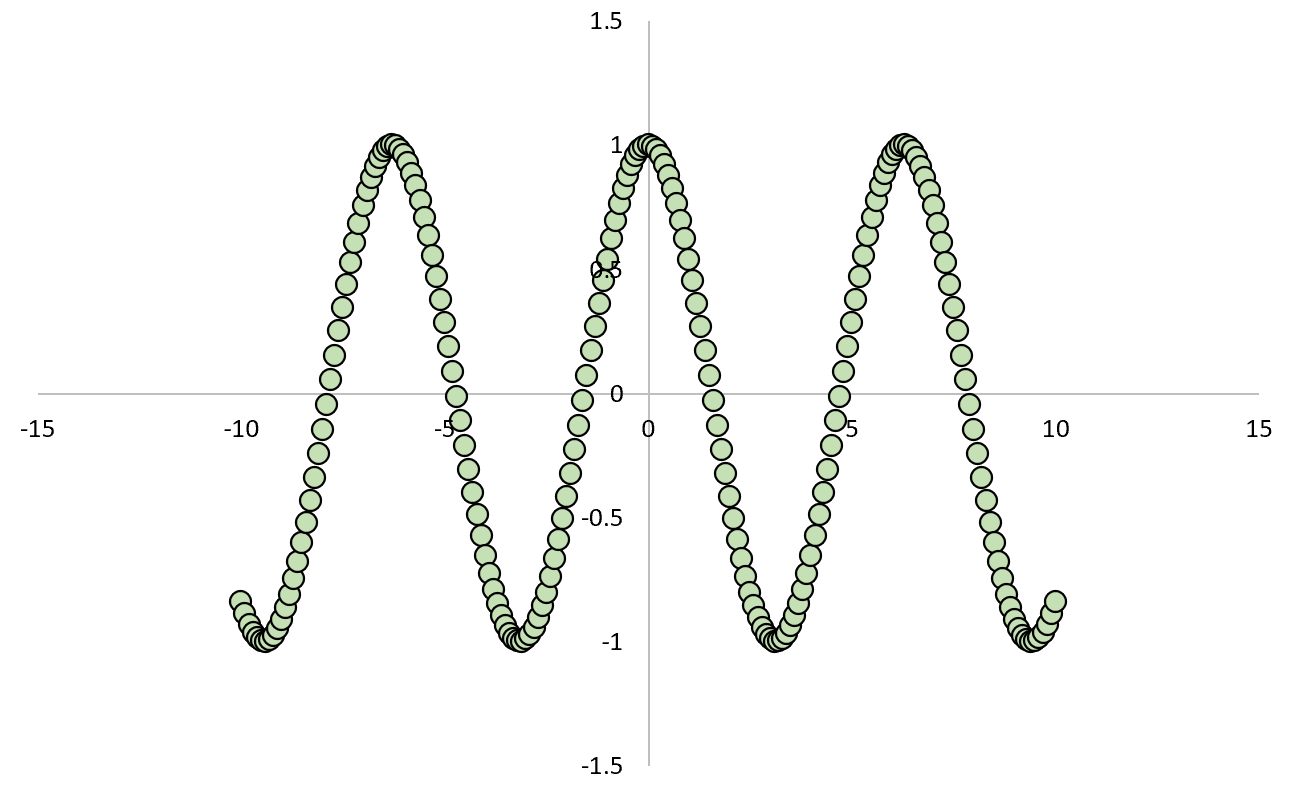
If we calculated the between the two variables, we would find that the correlation is zero.

We know that X causes Y, but the linear correlation between the two variables is zero.

The following tutorials provide additional information about correlation and causation: