Table of Contents
Multiple linear regression by hand is a step-by-step process to calculate the coefficients of multiple independent variables used to predict a dependent variable. It involves estimating the parameters of a linear equation, which requires finding the mean, variance, and covariance of the variables, calculating the regression coefficients, and testing the significance of the model. This process follows a number of steps, such as forming the linear equation, taking the partial derivatives of the cost function, setting the derivatives to zero, and solving to find the coefficients.
Multiple linear regression is a method we can use to quantify the relationship between two or more predictor variables and a response variable.
This tutorial explains how to perform multiple linear regression by hand.
Example: Multiple Linear Regression by Hand
Suppose we have the following dataset with one response variable y and two predictor variables X1 and X2:
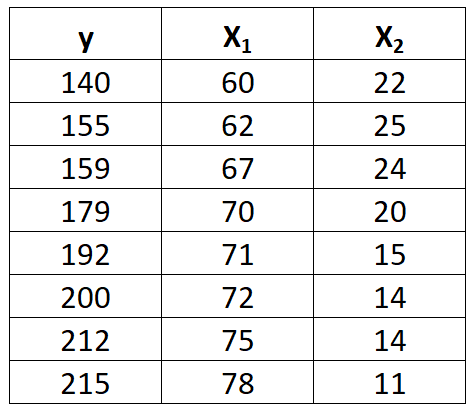
Use the following steps to fit a multiple linear regression model to this dataset.
Step 1: Calculate X12, X22, X1y, X2y and X1X2.
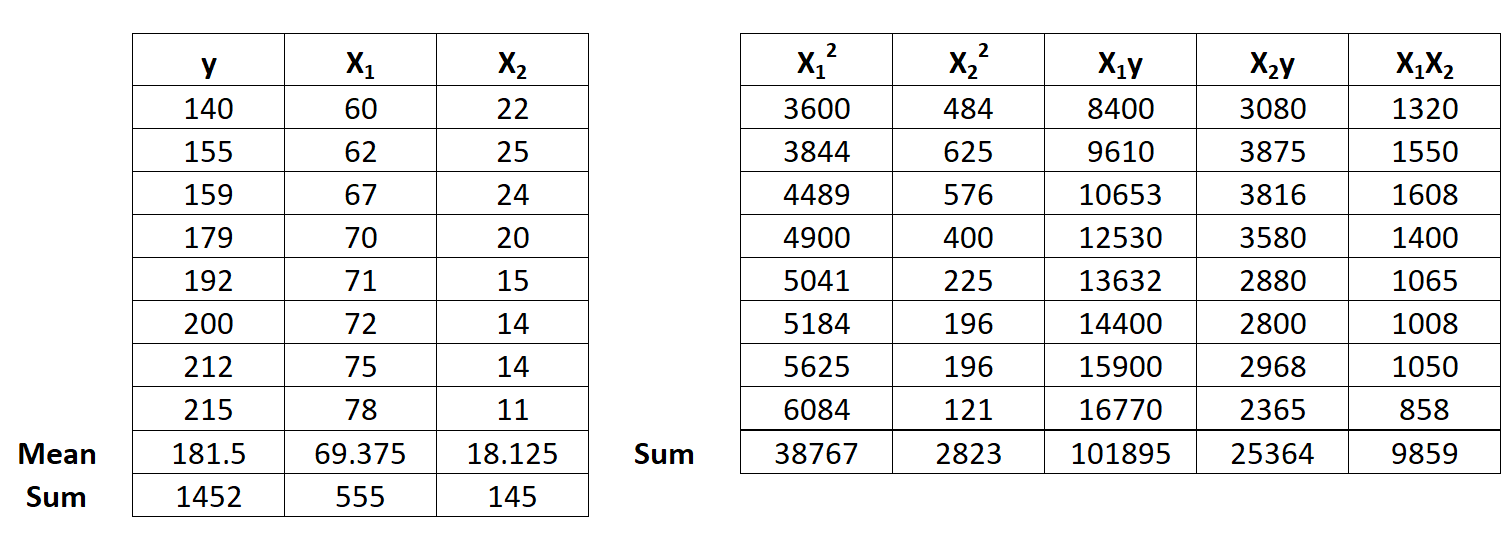
Step 2: Calculate Regression Sums.
Next, make the following regression sum calculations:
- Σx12 = ΣX12 – (ΣX1)2 / n = 38,767 – (555)2 / 8 = 263.875
- Σx22 = ΣX22 – (ΣX2)2 / n = 2,823 – (145)2 / 8 = 194.875
- Σx1y = ΣX1y – (ΣX1Σy) / n = 101,895 – (555*1,452) / 8 = 1,162.5
- Σx2y = ΣX2y – (ΣX2Σy) / n = 25,364 – (145*1,452) / 8 = -953.5
- Σx1x2 = ΣX1X2 – (ΣX1ΣX2) / n = 9,859 – (555*145) / 8 = -200.375
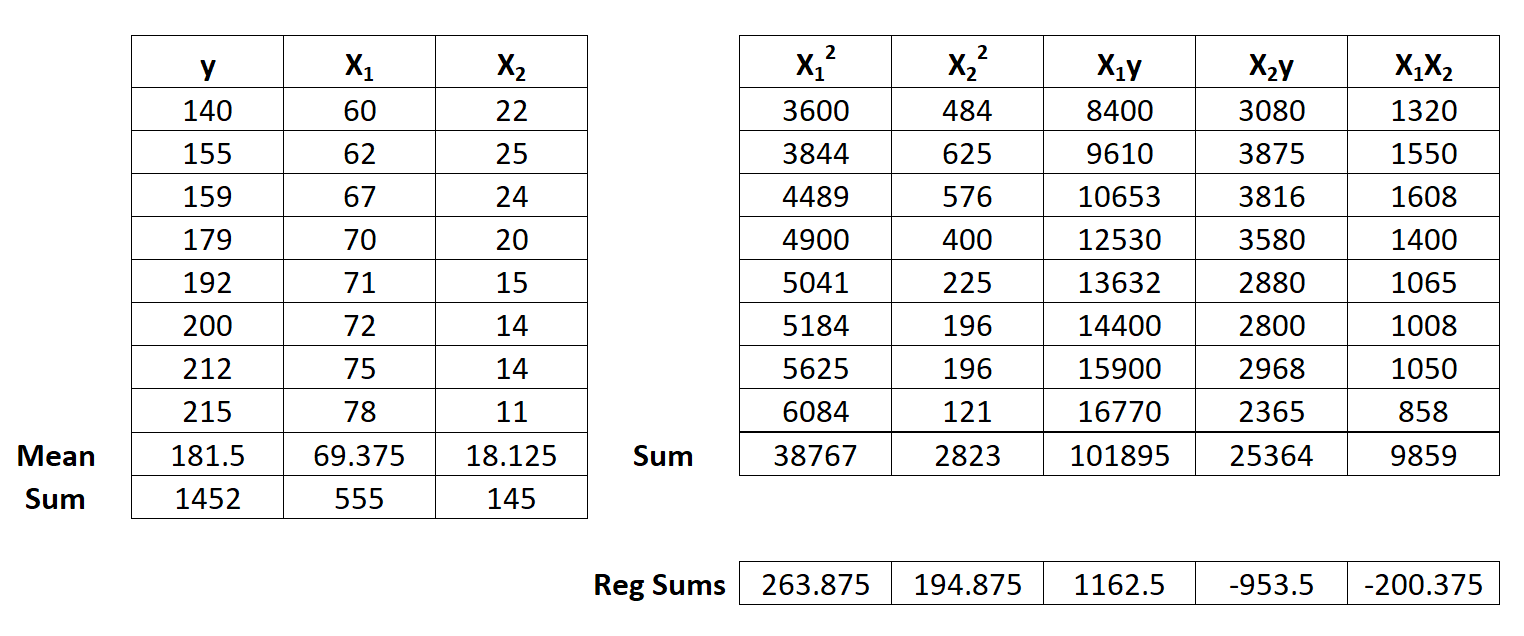
Step 3: Calculate b0, b1, and b2.
The formula to calculate b1 is: [(Σx22)(Σx1y) – (Σx1x2)(Σx2y)] / [(Σx12) (Σx22) – (Σx1x2)2]
Thus, b1 = [(194.875)(1162.5) – (-200.375)(-953.5)] / [(263.875) (194.875) – (-200.375)2] = 3.148
The formula to calculate b2 is: [(Σx12)(Σx2y) – (Σx1x2)(Σx1y)] / [(Σx12) (Σx22) – (Σx1x2)2]
Thus, b2 = [(263.875)(-953.5) – (-200.375)(1152.5)] / [(263.875) (194.875) – (-200.375)2] = -1.656
Thus, b0 = 181.5 – 3.148(69.375) – (-1.656)(18.125) = -6.867
Step 5: Place b0, b1, and b2 in the estimated linear regression equation.
The estimated linear regression equation is: ŷ = b0 + b1*x1 + b2*x2
In our example, it is ŷ = -6.867 + 3.148x1 – 1.656x2
How to Interpret a Multiple Linear Regression Equation
Here is how to interpret this estimated linear regression equation: ŷ = -6.867 + 3.148x1 – 1.656x2
b0 = -6.867. When both predictor variables are equal to zero, the mean value for y is -6.867.
b1 = 3.148. A one unit increase in x1 is associated with a 3.148 unit increase in y, on average, assuming x2 is held constant.
b2 = -1.656. A one unit increase in x2 is associated with a 1.656 unit decrease in y, on average, assuming x1 is held constant.
An Introduction to Multiple Linear Regression
How to Perform Simple Linear Regression by Hand
