Table of Contents
Multiple linear regression (MLR) is a statistical technique used to predict a response variable based on multiple predictor variables. It is based on five assumptions: (1) linearity, (2) homoscedasticity, (3) normality of residuals, (4) independence of observations, and (5) lack of multicollinearity. These assumptions must be met for MLR to be valid. In addition, the relationships between predictor and response variables must be linear to ensure accurate and reliable results.
is a statistical method we can use to understand the relationship between multiple predictor variables and a .
However, before we perform multiple linear regression, we must first make sure that five assumptions are met:
1. Linear relationship: There exists a linear relationship between each predictor variable and the response variable.
2. No Multicollinearity: None of the predictor variables are highly correlated with each other.
3. Independence: The observations are independent.
4. Homoscedasticity: The residuals have constant variance at every point in the linear model.
5. Multivariate Normality: The residuals of the model are normally distributed.
If one or more of these assumptions are violated, then the results of the multiple linear regression may be unreliable.
In this article, we provide an explanation for each assumption, how to determine if the assumption is met, and what to do if the assumption is violated.
Assumption 1: Linear Relationship
Multiple linear regression assumes that there is a linear relationship between each predictor variable and the response variable.
How to Determine if this Assumption is Met
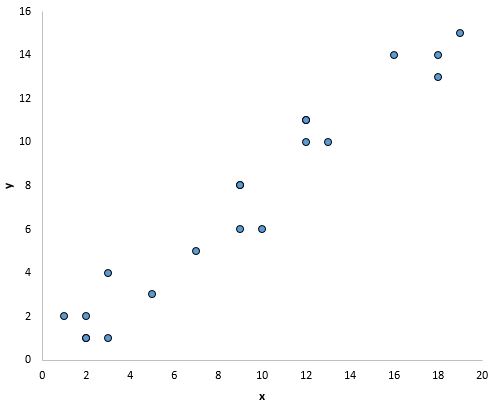
The easiest way to determine if this assumption is met is to create a scatter plot of each predictor variable and the response variable.
This allows you to visually see if there is a linear relationship between the two variables.
If the points in the scatter plot roughly fall along a straight diagonal line, then there likely exists a linear relationship between the variables.
For example, the points in the plot below look like they fall on roughly a straight line, which indicates that there is a linear relationship between this particular predictor variable (x) and the response variable (y):
What to Do if this Assumption is Violated
If there is not a linear relationship between one or more of the predictor variables and the response variable, then we have a couple options:
1. Apply a nonlinear transformation to the predictor variable such as taking the log or the square root. This can often transform the relationship to be more linear.
2. Add another predictor variable to the model. For example, if the plot of x vs. y has a parabolic shape then it might make sense to add X2 as an additional predictor variable in the model.
3. Drop the predictor variable from the model. In the most extreme case, if there exists no linear relationship between a certain predictor variable and the response variable then the predictor variable may not be useful to include in the model.
Assumption 2: No Multicollinearity
Multiple linear regression assumes that none of the predictor variables are highly correlated with each other.
When one or more predictor variables are highly correlated, the regression model suffers from , which causes the coefficient estimates in the model to become unreliable.
How to Determine if this Assumption is Met
The easiest way to determine if this assumption is met is to calculate the VIF value for each predictor variable.
VIF values start at 1 and have no upper limit. As a general rule of thumb, VIF values greater than 5* indicate potential multicollinearity.
The following tutorials show how to calculate VIF in various statistical software:
* Sometimes researchers use a VIF value of 10 instead, depending on the field of study.
What to Do if this Assumption is Violated
If one or more of the predictor variables has a VIF value greater than 5, the easiest way to resolve this issue is to simply remove the predictor variable(s) with the high VIF values.
Alternatively, if you want to keep each predictor variable in the model then you can use a different statistical method such as , , or that is designed to handle predictor variables that are highly correlated.
Assumption 3: Independence
Multiple linear regression assumes that each observation in the dataset is independent.
How to Determine if this Assumption is Met
The simplest way to determine if this assumption is met is to perform a , which is a formal statistical test that tells us whether or not the residuals (and thus the observations) exhibit autocorrelation.
What to Do if this Assumption is Violated
Depending on the nature of the way this assumption is violated, you have a few options:
- For positive serial correlation, consider adding lags of the dependent and/or independent variable to the model.
- For negative serial correlation, check to make sure that none of your variables are overdifferenced.
- For seasonal correlation, consider adding seasonal to the model.
Assumption 4: Homoscedasticity
Multiple linear regression assumes that the residuals have constant variance at every point in the linear model. When this is not the case, the residuals are said to suffer from .
When heteroscedasticity is present in a regression analysis, the results of the regression model become unreliable.
Specifically, heteroscedasticity increases the variance of the regression coefficient estimates, but the regression model doesn’t pick up on this. This makes it much more likely for a regression model to declare that a term in the model is statistically significant, when in fact it is not.
How to Determine if this Assumption is Met
The simplest way to determine if this assumption is met is to create a plot of standardized residuals versus predicted values.
Once you fit a regression model to a dataset, you can then create a scatter plot that shows the predicted values for the response variable on the x-axis and the standardized residuals of the model on the y-axis.
If the points in the scatter plot exhibit a pattern, then heteroscedasticity is present.
The following plot shows an example of a regression model where heteroscedasticity is not a problem:
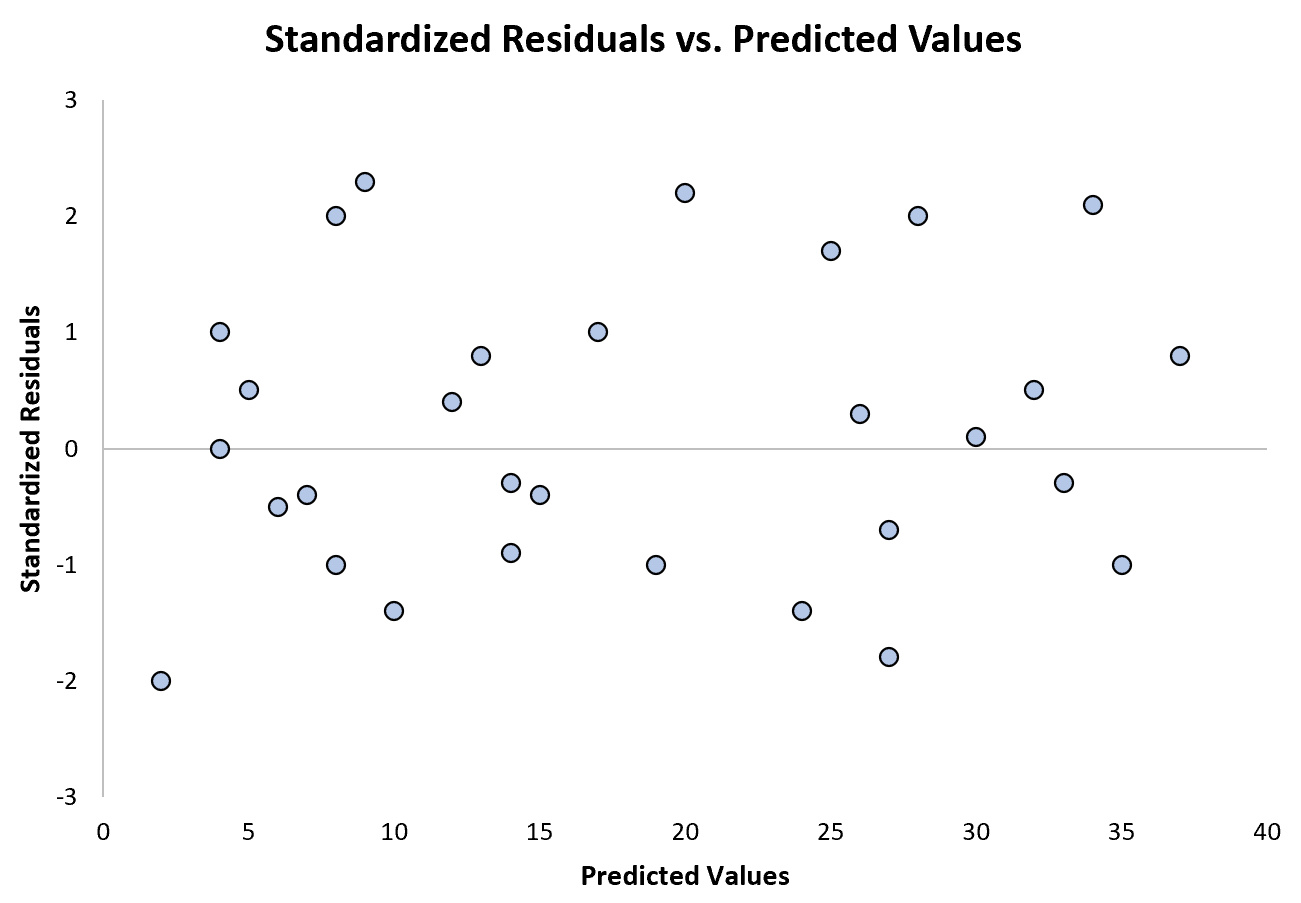
Notice that the standardized residuals are scattered about zero with no clear pattern.
The following plot shows an example of a regression model where heteroscedasticity is a problem:
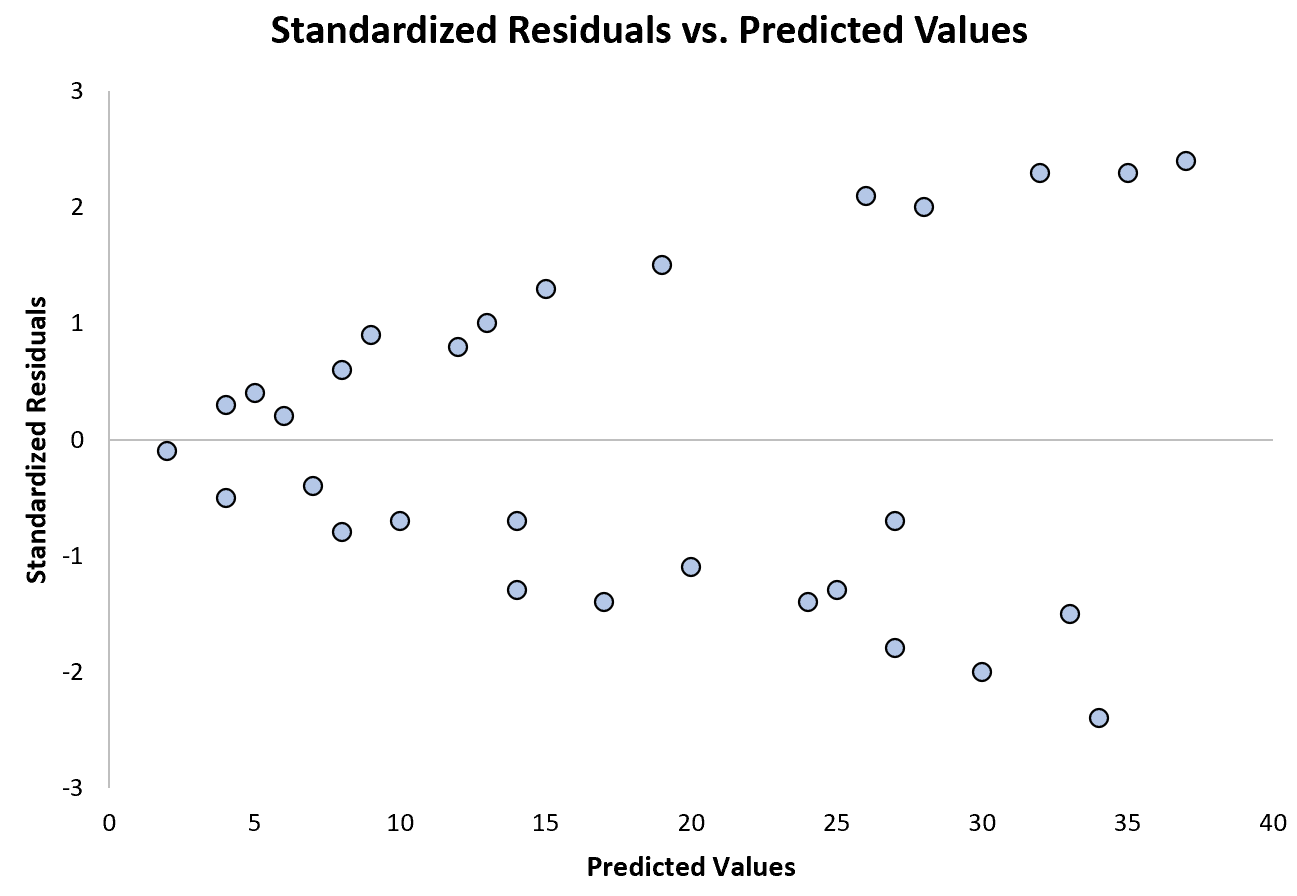
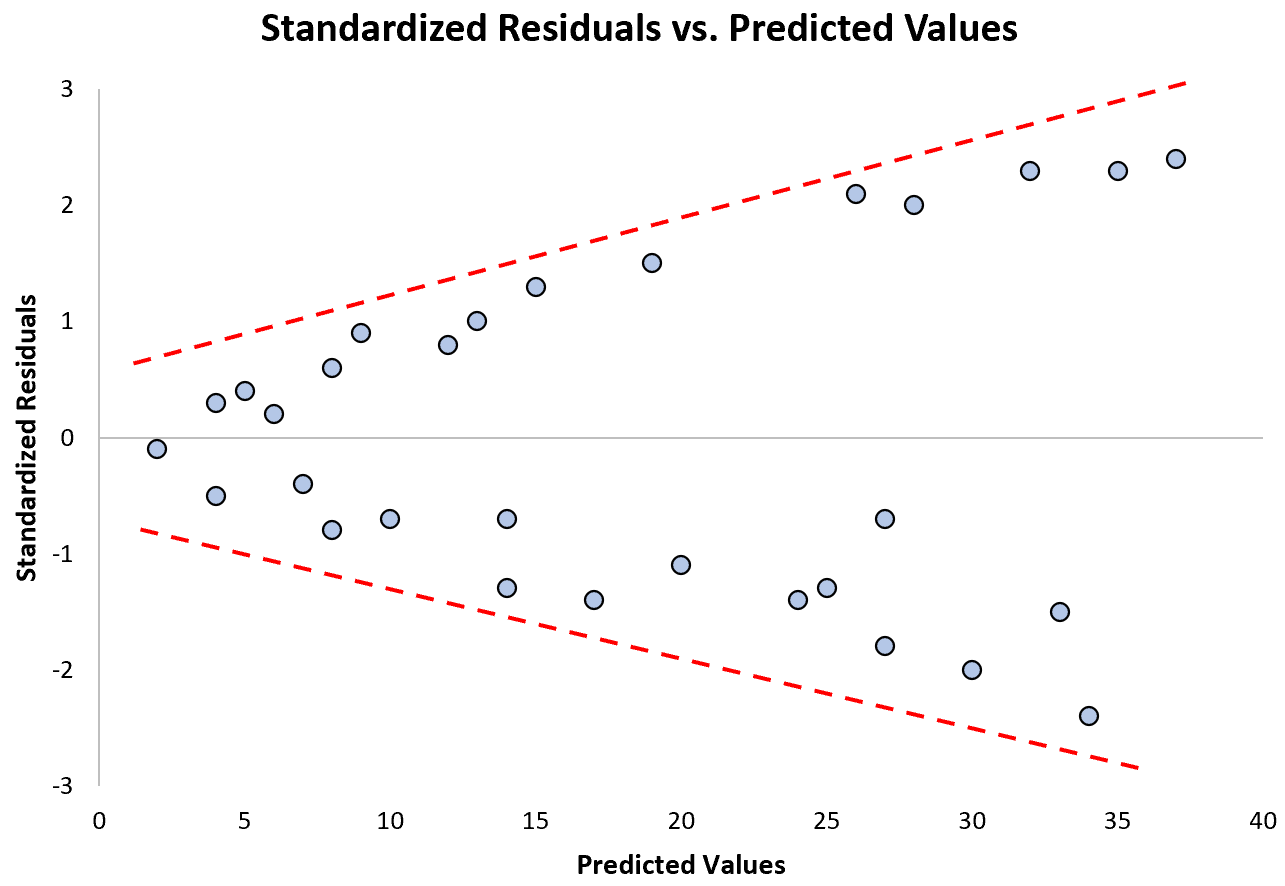
Notice how the standardized residuals become much more spread out as the predicted values get larger. This “cone” shape is a classic sign of heteroscedasticity:
What to Do if this Assumption is Violated
There are three common ways to fix heteroscedasticity:
1. Transform the response variable. The most common way to deal with heteroscedasticity is to transform the response variable by taking the log, square root, or cube root of all of the values of the response variable. This often causes heteroscedasticity to go away.
2. Redefine the response variable. One way to redefine the response variable is to use a rate, rather than the raw value. For example, instead of using the population size to predict the number of flower shops in a city, we may instead use population size to predict the number of flower shops per capita.
In most cases, this reduces the variability that naturally occurs among larger populations since we’re measuring the number of flower shops per person, rather than the sheer amount of flower shops.
3. Use weighted regression. Another way to fix heteroscedasticity is to use weighted regression, which assigns a weight to each data point based on the variance of its fitted value.
Essentially, this gives small weights to data points that have higher variances, which shrinks their squared residuals. When the proper weights are used, this can eliminate the problem of heteroscedasticity.
Related:
Assumption 4: Multivariate Normality
Multiple linear regression assumes that the residuals of the model are normally distributed.
How to Determine if this Assumption is Met
There are two common ways to check if this assumption is met:
1. Check the assumption visually using .
A Q-Q plot, short for quantile-quantile plot, is a type of plot that we can use to determine whether or not the residuals of a model follow a normal distribution. If the points on the plot roughly form a straight diagonal line, then the normality assumption is met.
The following Q-Q plot shows an example of residuals that roughly follow a normal distribution:
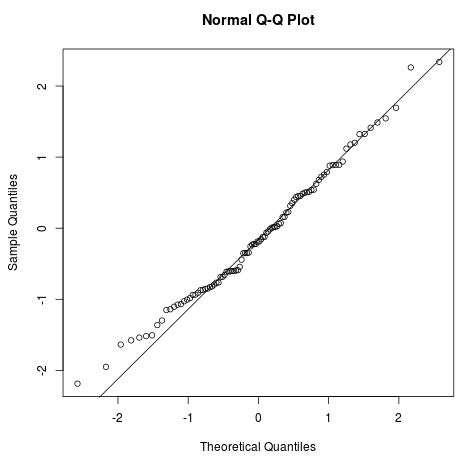
However, the Q-Q plot below shows an example of when the residuals clearly depart from a straight diagonal line, which indicates that they do not follow normal distribution:
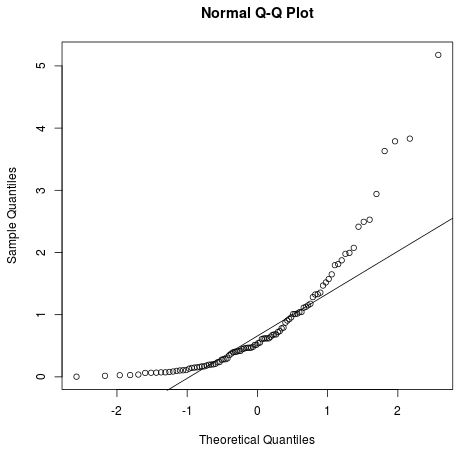
2. Check the assumption using a formal statistical test like Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre, or D’Agostino-Pearson.
Keep in mind that these tests are sensitive to large sample sizes – that is, they often conclude that the residuals are not normal when your sample size is extremely large. This is why it’s often easier to use graphical methods like a Q-Q plot to check this assumption.
What to Do if this Assumption is Violated
If the normality assumption is violated, you have a couple options:
1. First, verify that there are no extreme outliers present in the data that cause the normality assumption to be violated.
2. Next, you can apply a nonlinear transformation to the response variable such as taking the square root, the log, or the cube root of all of the values of the response variable. This often causes the residuals of the model to become more normally distributed.
The following tutorials provide additional information about multiple linear regression and its assumptions:
The following tutorials provide step-by-step examples of how to perform multiple linear regression using different statistical software:
