Table of Contents
Performing a Chi-Square Test of Independence in SAS requires running a PROC FREQ procedure to obtain the cross tabulation of two categorical variables. The result of the PROC FREQ procedure is then used to run a PROC CHISQ procedure to obtain the Chi-Square test statistic and the corresponding p-value. The p-value is then used to assess the statistical significance of the association between the two variables.
A Chi-Square Test of Independence is used to determine whether or not there is a significant association between two .
The following example shows how to perform a Chi-Square Test of Independence in SAS.
Example: Chi-Square Test of Independence in SAS
Suppose we want to know whether or not gender is associated with political party preference. We take a of 500 voters and survey them on their political party preference.
The following table shows the results of the survey:
| Republican | Democrat | Independent | Total | |
| Male | 120 | 90 | 40 | 250 |
| Female | 110 | 95 | 45 | 250 |
| Total | 230 | 185 | 85 | 500 |
Use the following steps to perform a Chi-Square Test of Independence in SAS to determine if gender is associated with political party preference.
Step 1: Create the data.
First, we will create a dataset in SAS to hold the survey responses:
/*create dataset*/ data my_data; input Gender $ Party $ Count; datalines; Male Rep 120 Male Dem 90 Male Ind 40 Female Rep 110 Female Dem 95 Female Ind 45 ; run; /*print dataset*/ proc print data=my_data;
Step 2: Perform the Chi-Square Test of Independence.
Next, we can use the following code to perform the Chi-Square Test of Independence:
/*perform Chi-Square Test of Independence*/ proc freq data=my_data; tables Gender*Party / chisq; weight Count; run;
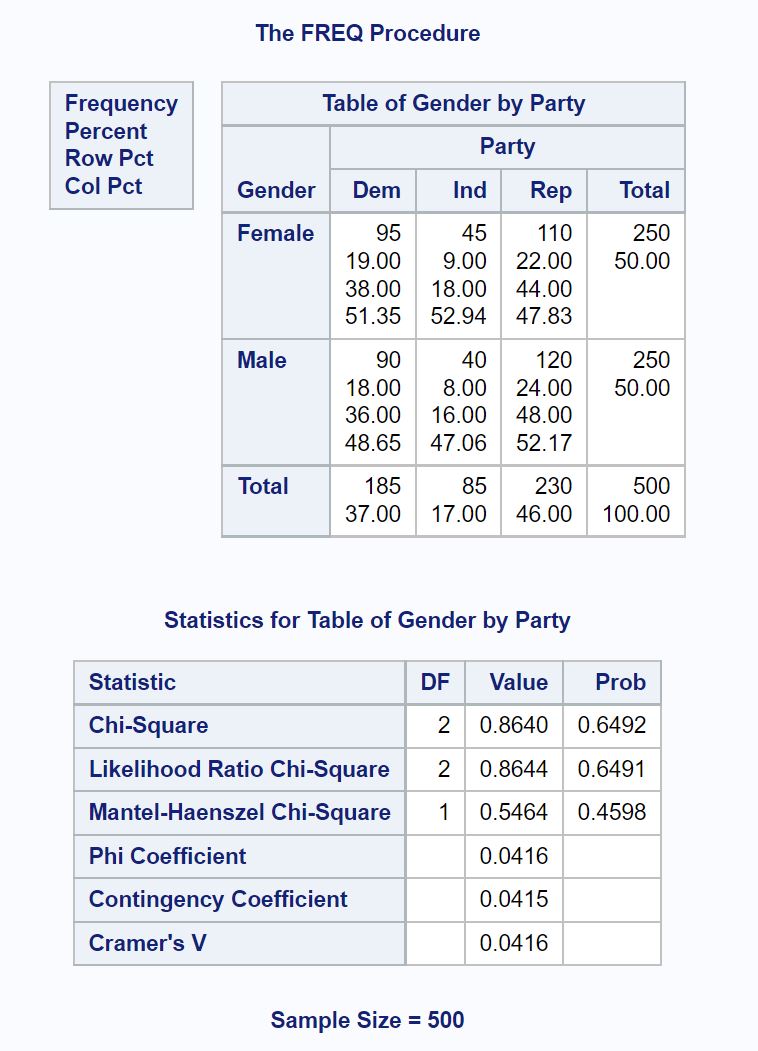
There are two values of interest in the output:
- Chi-Square Test Statistic: 0.8640
- Corresponding p-value: 0.6492
- H0: The two variables are independent.
- HA: The two variables are not independent.
Since the (0.6492) of the test is not less than 0.05, we fail to reject the null hypothesis.
This means we do not have sufficient evidence to say that there is an association between gender and political party preference.
In other words, gender and political party preference are independent.
The following tutorials provide additional information about the Chi-Square test of independence:
