How to perform a One Sample t-test on a TI-84 Calculator ?

---

A  is used to test whether or not the mean of a population is equal to some value.

This tutorial explains how to conduct a one sample t-test on a TI-84 calculator.

Example: One Sample t-test on a TI-84 Calculator

Researchers want to know if a certain type of car gets 20 miles per gallon or not. They obtain a random sample of 74 cars and find that the mean is 21.29 mpg while the standard deviation is 5.78 mpg. Use this data to perform a one sample t-test to determine if the true mpg for this type of car is equal to 20 mpg.

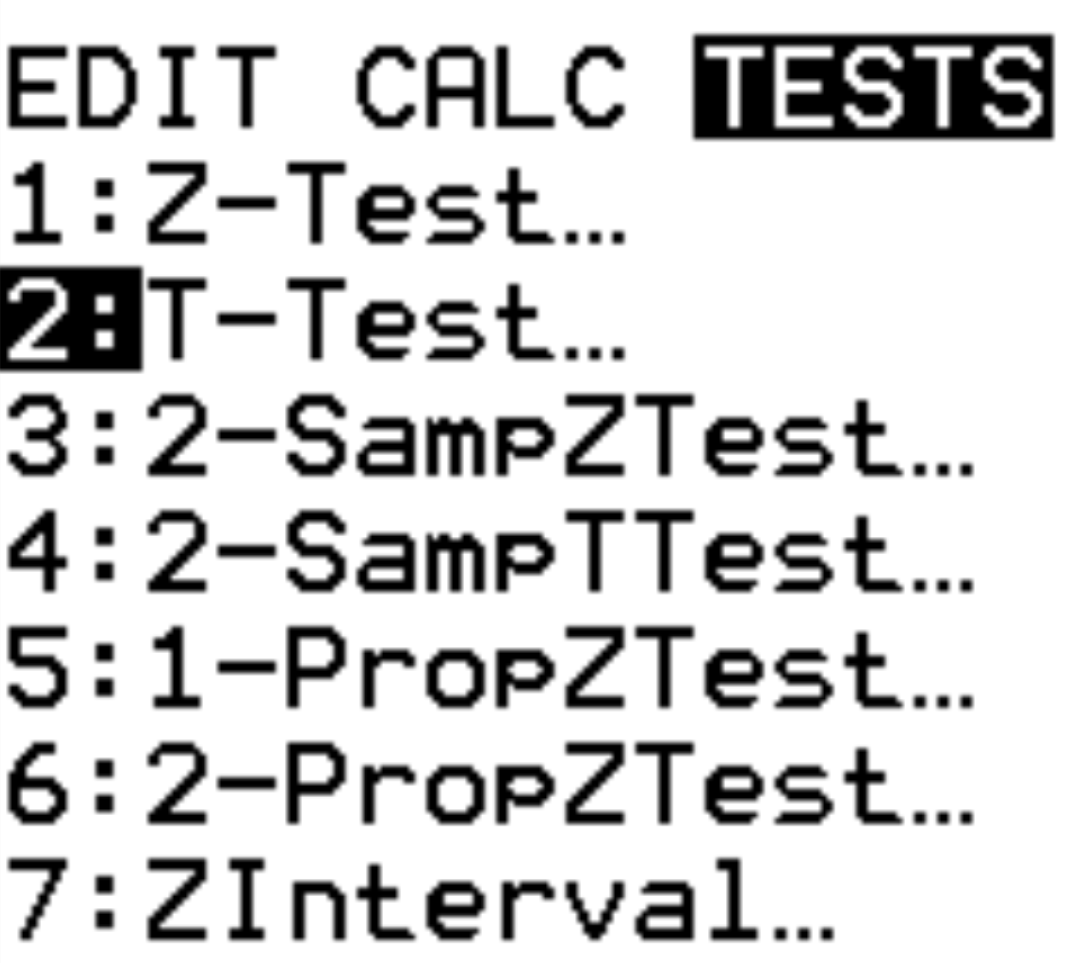
Step 1: Select T-Test.

Press Stat. Scroll over to TESTS. Scroll down to T-Test and press ENTER.

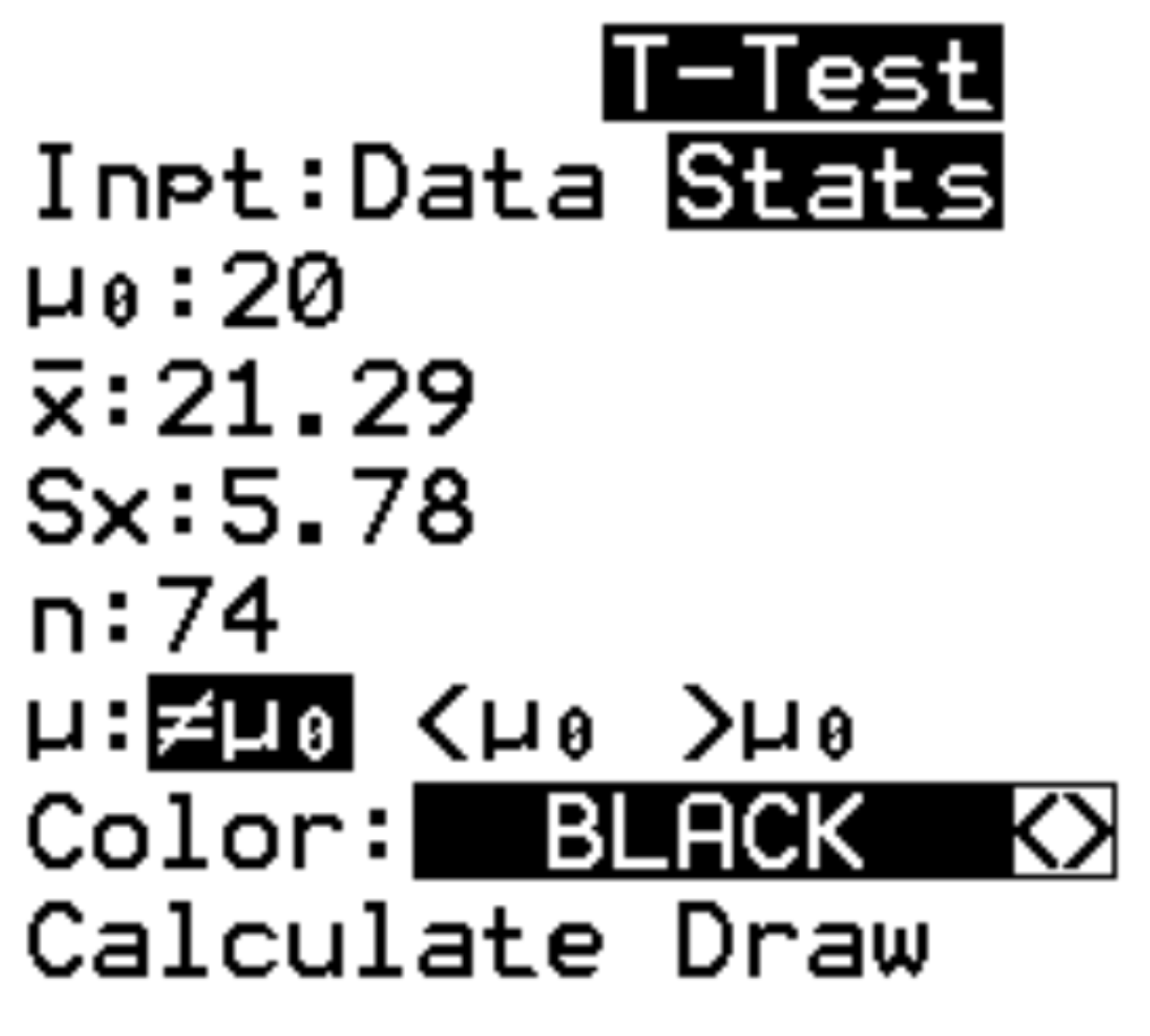
Step 2: Fill in the necessary info.

The calculator will ask for the following information:

• Inpt: Choose whether you are working with raw data (Data) or summary statistics (Stats). In this case, we will highlight Stats and press ENTER.
• μ₀: The mean to be used in the null hypothesis. We will type 20 and press  ENTER.
• x: The sample mean. We will type 21.29 and press  ENTER.
• s_x: The sample standard deviation. We will type 5.78 and press ENTER.
• n: The sample size. We will type 74 and press ENTER.
• μ:The alternative hypothesis to be used. Since we are performing a two-tailed test, we will highlight ≠μ₀ and press ENTER. This indicates that our alternative hypothesis is μ≠20. The other two options would be used for left-tailed tests (<μ₀) and right-tailed tests (>μ₀) .

Lastly, highlight Calculate and press ENTER.

Step 3: Interpret the results.

Our calculator will automatically produce the results of the one-sample t-test:

Here is how to interpret the results:

• μ≠20: This is the alternative hypothesis for the test.
• t=1.919896124: This is the t test-statistic. 
• p=0.0587785895: This is the p-value that corresponds to the test-statistic.
• x=21.59. This is the sample mean that we entered.
• s_x=5.78. This is the sample standard deviation that we entered.
• n=74: This is the sample size that we entered.