Table of Contents
A Chi-Square Test of Independence on a TI-84 Calculator is a way to determine whether there is a statistically significant relationship between two categorical variables. To perform this test, you will need to enter the observed values of the two variables into a 2×2 table, and then use the TI-84 calculator to calculate the Chi-Square statistic. The calculator will then output the p-value associated with the statistic, which will tell you the probability that the two variables are independent.
A is used to determine whether or not there is a significant association between two categorical variables.
This tutorial explains how to perform a Chi-Square Test of Independence on a TI-84 Calculator.
Example: Chi-Square Test of Independence on a TI-84 Calculator
Suppose we want to know whether or not gender is associated with political party preference. We take a simple random sample of 500 voters and survey them on their political party preference. The following table shows the results of the survey:
| Republican | Democrat | Independent | Total | |
| Male | 120 | 90 | 40 | 250 |
| Female | 110 | 95 | 45 | 250 |
| Total | 230 | 185 | 85 | 500 |
Use the following steps to perform a Chi-Square test of independence to determine if gender is associated with political party preference.
Step 1: Input the data.
First, we will input the data into a matrix. Press 2nd and then press x-1 . Scroll over to Edit, highlight any matrix that is blank and press Enter. Then, choose the number of rows (2 in our case) and columns (3 in our case) to use in the matrix and enter the raw data:

Step 2: Perform a Chi-Square Test of Independence.
Next, we will perform a Chi-Square test of independence on the matrix we just created. Press stat and scroll over to TESTS. Then scroll down to X2-Test and Press Enter.
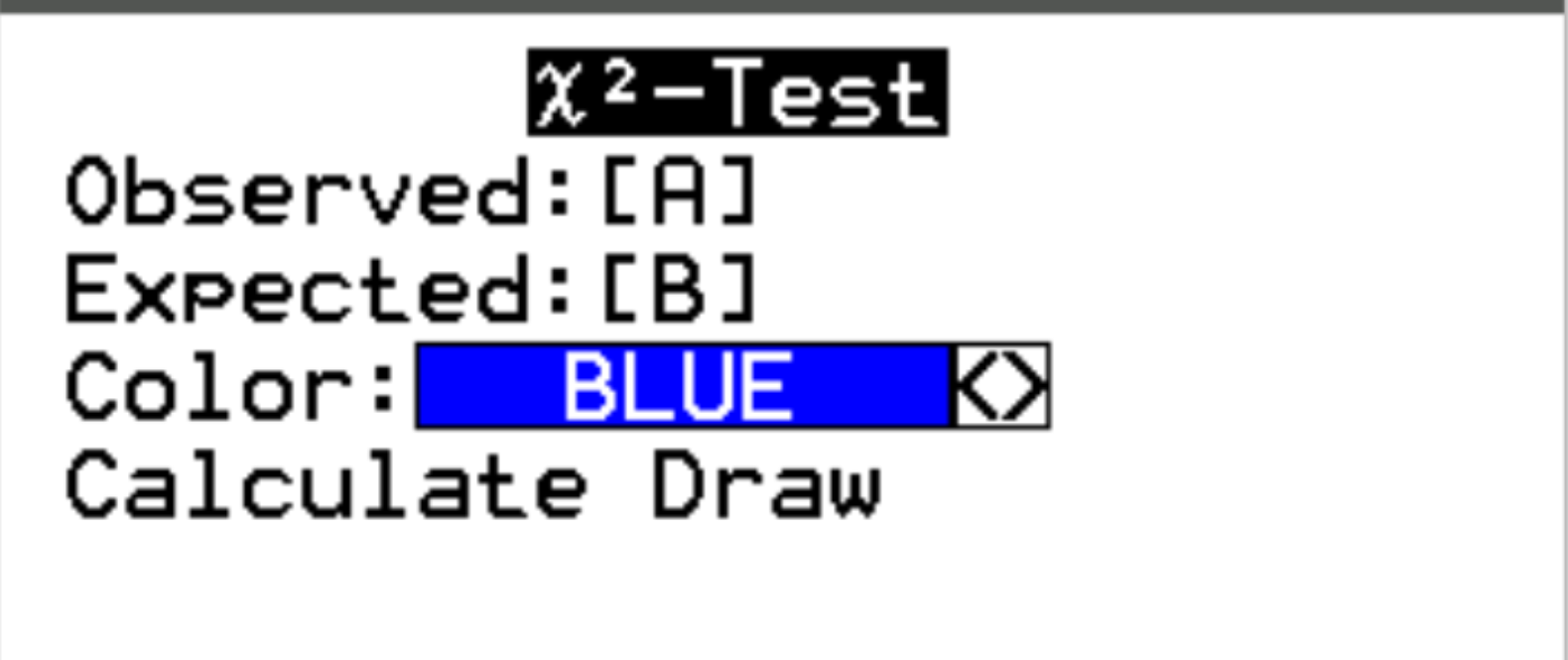
For Observed, choose the matrix you entered the data in. In our case, we used matrix A. For Expected, this can be any empty matrix (the calculator will automatically produce the expected values for us). In our case, we’ll leave this as matrix B.
Then, highlight Calculate and press Enter.
The following output will automatically display:
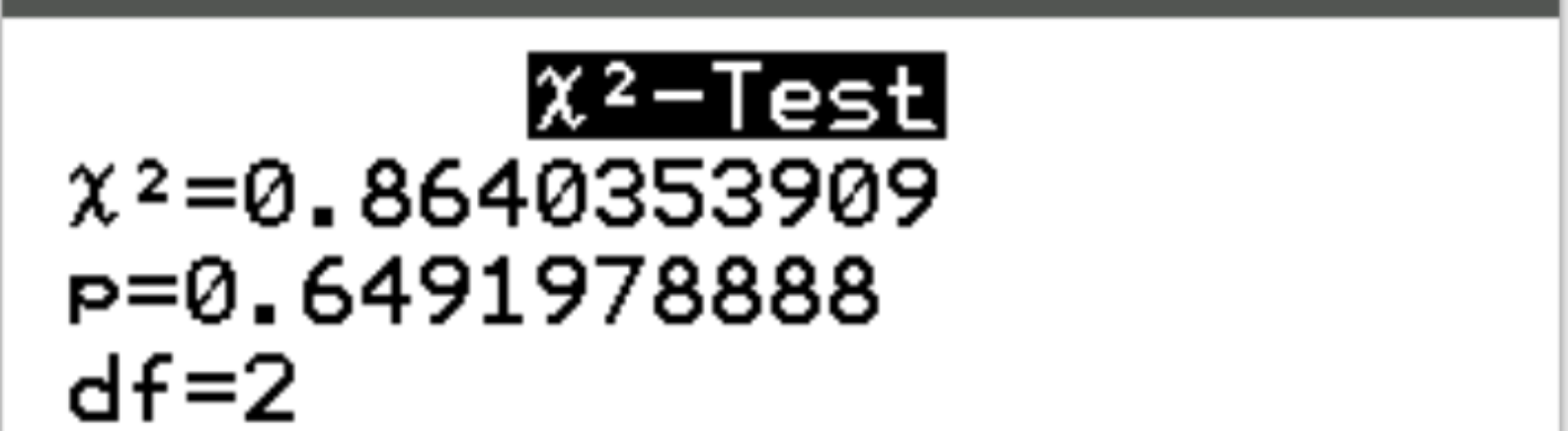
The X2 test statistic is 0.8640 and the corresponding p-value is 0.6492. Since this p-value is not less than .05, we fail to reject the null hypothesis. This means we do not have sufficient evidence to state that there is an association between gender and political party preference.
