Table of Contents
Performing linear regression on a TI-84 calculator can be done by first entering the data into the list editor, followed by selecting ‘STAT’ and then ‘CALC’. Selecting ‘LinReg(ax+b)’ will produce a summary of the linear equation, as well as the r-squared value. This summary can then be used to interpret the data and draw conclusions.
Linear regression is a method we can use to understand the relationship between an explanatory variable, x, and a response variable, y.
This tutorial explains how to perform linear regression on a TI-84 calculator.
Example: Linear Regression on a TI-84 Calculator
Suppose we are interested in understanding the relationship between the number of hours a student studies for an exam and the exam score they receive.
To explore this relationship, we can perform the following steps on a TI-84 calculator to conduct a simple linear regression using hours studied as an explanatory variable and exam score as a response variable.
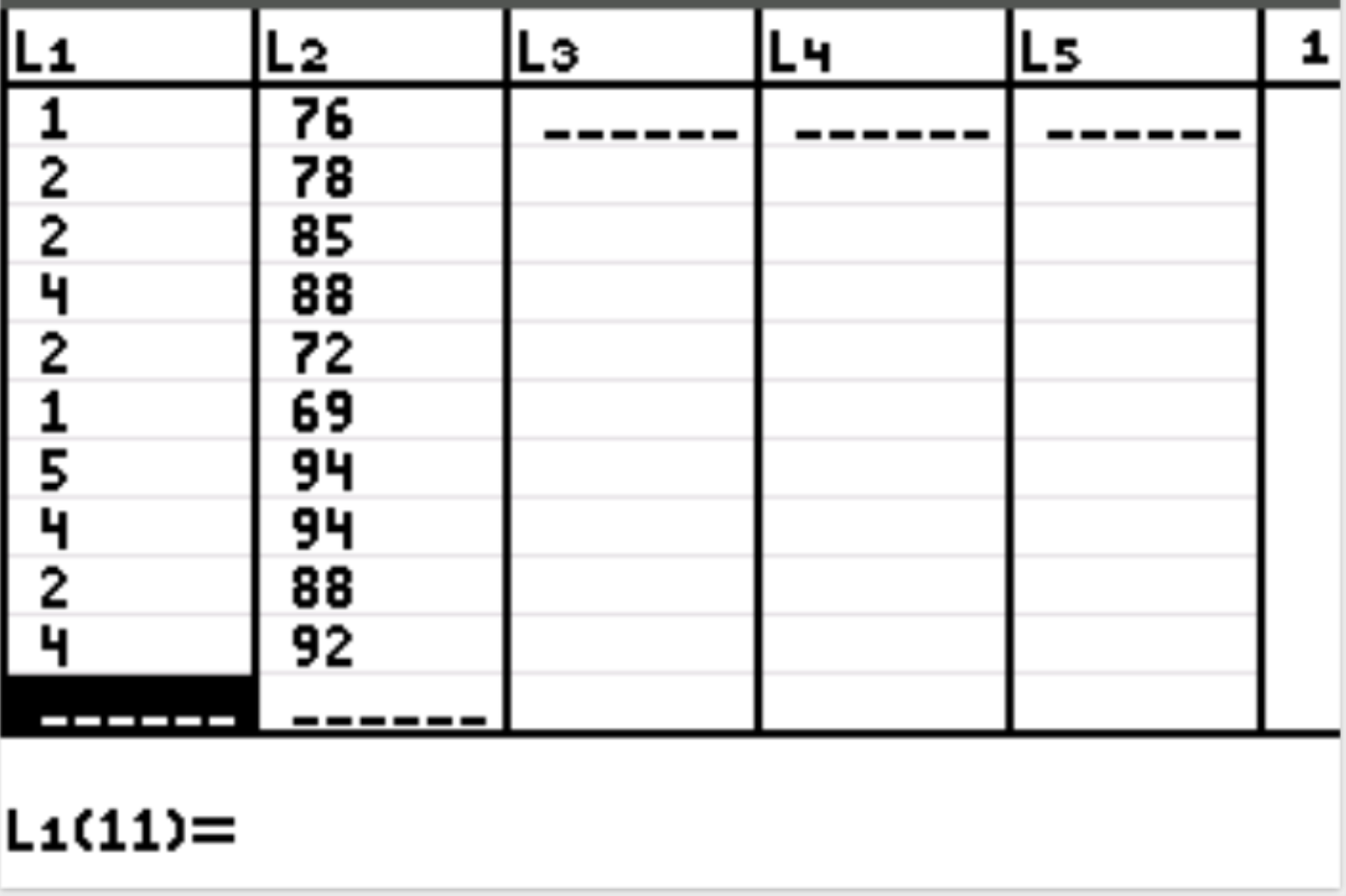
Step 1: Input the data.
First, we will input the data values for both the explanatory and the response variable. Press Stat and then press EDIT . Enter the following values for the explanatory variable (hours studied) in column L1 and the values for the response variable (exam score) in column L2:
Step 2: Perform linear regression.
Next, we will perform linear regression. Press Stat and then scroll over to CALC. Then scroll down to 8: Linreg(a+bx) and press Enter.
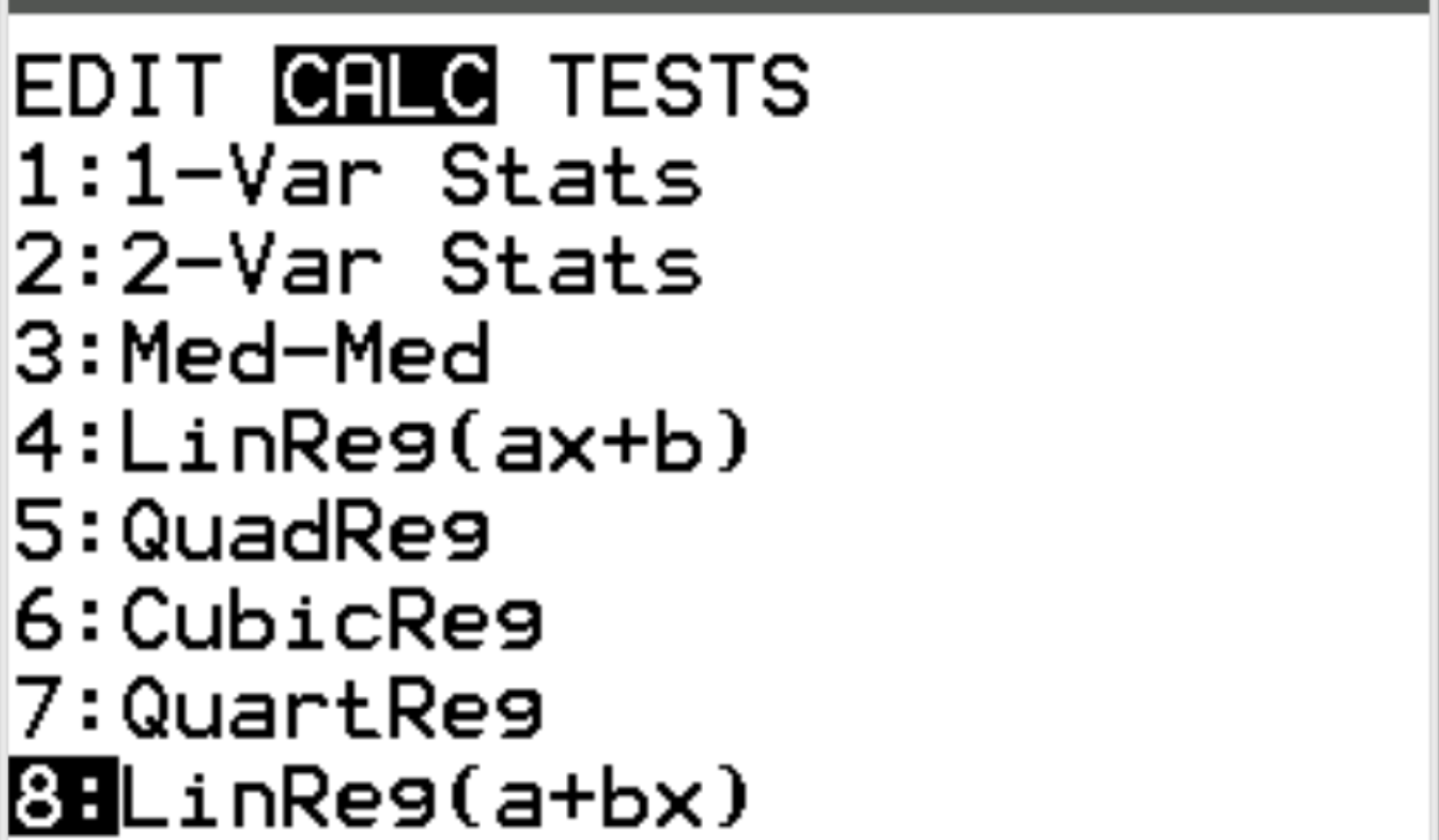
For Xlist and Ylist, make sure L1 and L2 are selected since these are the columns we used to input our data. Leave FreqList blank. Scroll down to Calculate and press Enter. The following output will automatically appear:
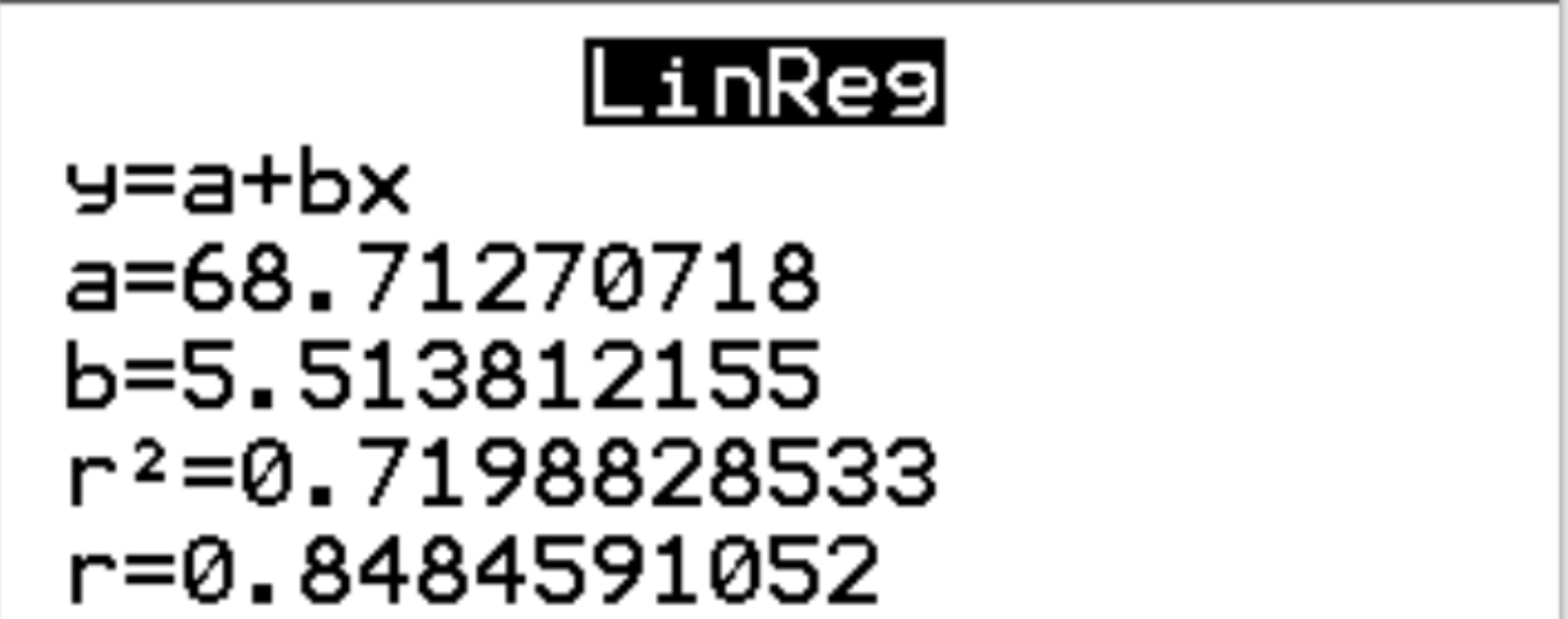
Step 3: Interpret the results.
From the results, we can see that the estimated regression equation is as follows:
exam score = 68.7127 + 5.5138*(hours)
We interpret the coefficient for hours to mean that for each additional hour studied, the exam score is expected to increase by 5.5138, on average. We interpret the coefficient for the intercept to mean that the expected exam score for a student who studies zero hours is 68.7127.
For example, a student who studies for three hours is expected to receive an exam score of 85.25:
exam score = 68.7127 + 5.5138*(3) = 85.25
We can also see that the r-squared for the regression model is r2 = 0.7199.
This value is known as the coefficient of determination. It is the proportion of the variance in the response variable that can be explained by the explanatory variable. In this example, 71.99% of the variation in the exam scores can be explained by the number of hours studied.
How to Create a Residual Plot on a TI-84 Calculator
