Table of Contents
To perform a Paired Samples t-test on a TI-84 Calculator, enter the paired sample data into the calculator, select “Stats”, select “Tests”, select “T Interval”, select “Paired”, enter the desired confidence level, and then press “Enter”. The calculator will then output the mean difference, t-statistic and the p-value for the test.
A is used to compare the means of two samples when each observation in one sample can be paired with an observation in the other sample.
This tutorial explains how to conduct a paired t-test on a TI-84 calculator.
Example: Paired samples t-test on a TI-84 Calculator
Researchers want to know if a new fuel treatment leads to a change in the average mpg of a certain car. To test this, they conduct an experiment in which they measure the mpg of 11 cars with and without the fuel treatment.
Since each car receives the treatment, we can conduct a paired t-test in which each car is paired with itself to determine if there is a difference in average mpg with and without the fuel treatment.
Perform the following steps to conduct a paired t-test on a TI-84 calculator.
Step 1: Input the data.
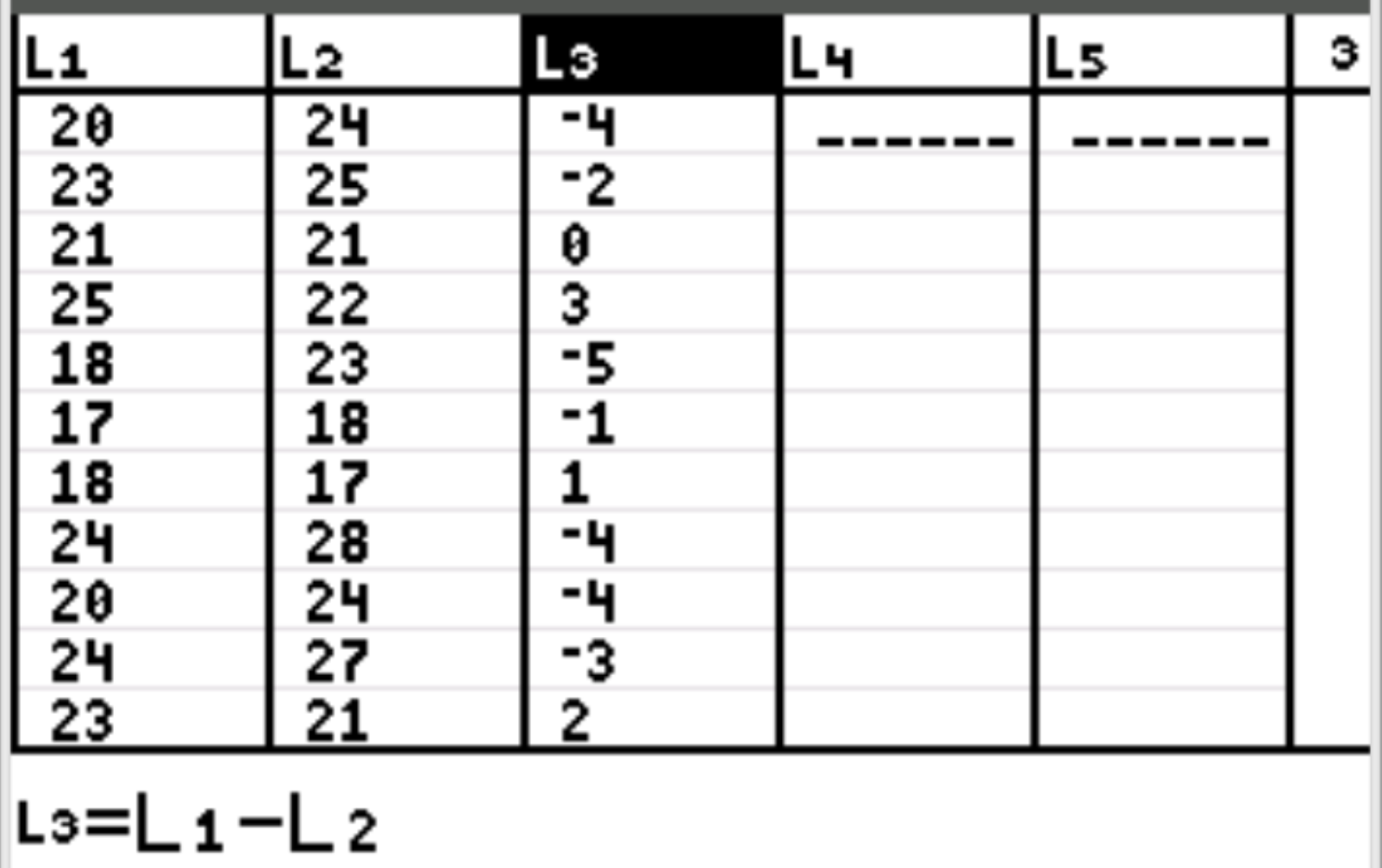
First, we will input the data values for both samples. Press Stat and then press EDIT . Enter the following values for the control group (no fuel treatment) in column L1 and the values for the treatment group variable (received fuel treatment) in column L2, followed by the difference between these two values in column L3.
Note: At the top of the third column, highlight L3. Then press 2nd and 1 to create L1, followed by a minus sign, then press 2nd and 2 to create L2. Then press Enter. Each of the values in column L3 will automatically populate using the formula L1-L2.
Step 2: Perform the paired t-test.
To perform the paired t-test, we will simply perform a t-test on column L3, which contains the values for the paired differences.
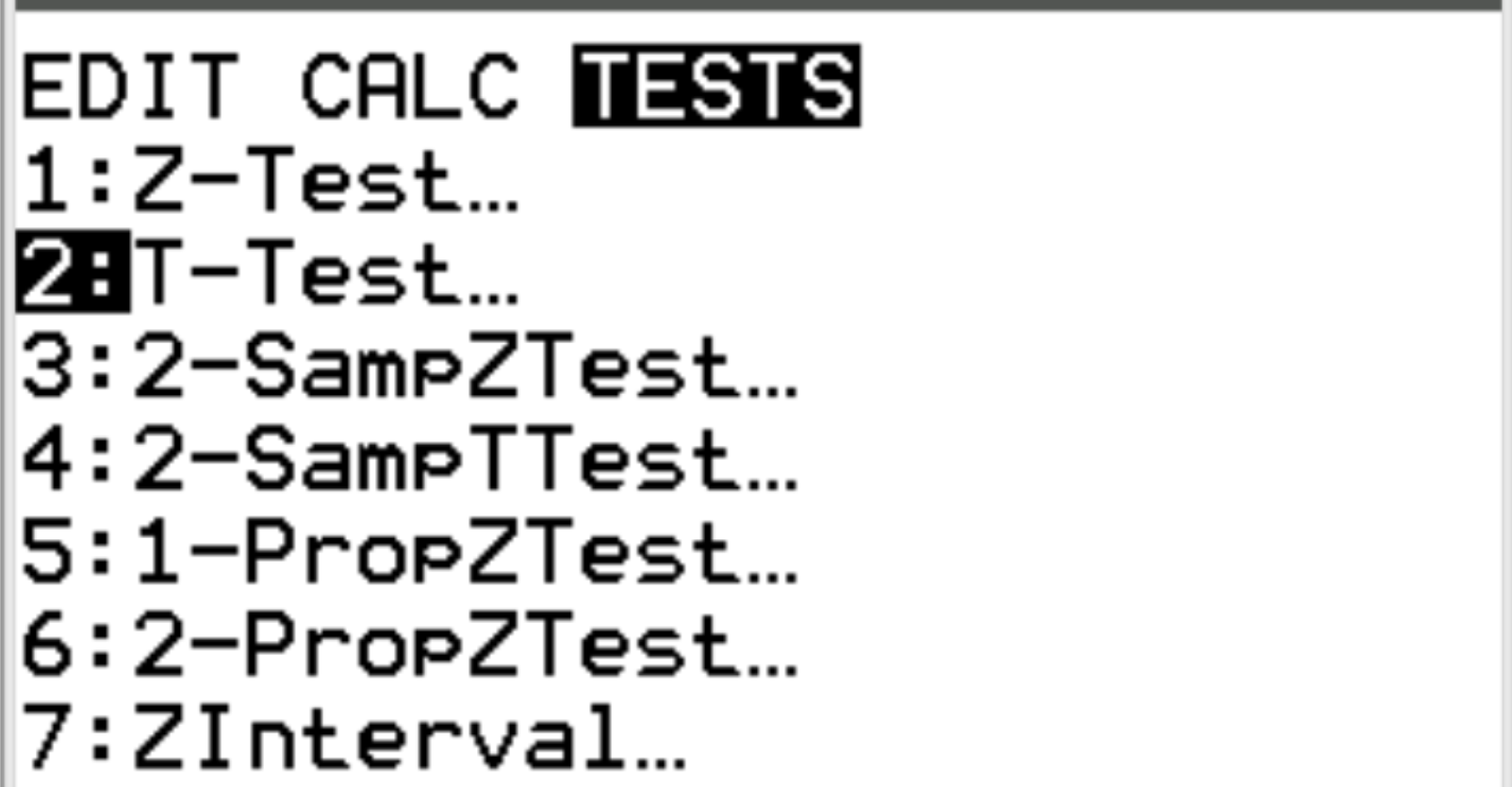
Press Stat. Scroll over to TESTS. Scroll down to 2:T-Test and press ENTER.
The calculator will ask for the following information:
- Inpt: Choose whether you are working with raw data (Data) or summary statistics (Stats). In this case, we will highlight Data and press ENTER.
- μ0: The mean difference to be used in the null hypothesis. We will type 0 and press ENTER.
- List: The list that contains the differences between the two samples. We will type L3 and press ENTER. Note: To get L3 to appear, press 2nd and then press 3.
- Freq: The frequency. Leave this set to 1.
- μ:The alternative hypothesis to be used. Since we are performing a two-tailed test, we will highlight ≠μ0 and press ENTER. This indicates that our alternative hypothesis is μ≠0. The other two options would be used for left-tailed tests (<μ0) and right-tailed tests (>μ0) .
Lastly, highlight Calculate and press ENTER.

Step 3: Interpret the results.
Our calculator will automatically produce the results of the one-sample t-test:

Here is how to interpret the results:
- μ≠0: This is the alternative hypothesis for the test.
- t=-1.8751: This is the t test-statistic.
- p=0.0903: This is the p-value that corresponds to the test-statistic.
- x=-1.5455. This is the mean difference of group 1 – group 2.
- sx=2.7336. This is the standard deviation of the differences.
- n=11: This is the total number of paired samples.
Because the of the test (0.0903) is not less than 0.05, we fail to reject the null hypothesis.
This means we do not have sufficient evidence to say that there is any difference between the average mpg of the two groups. That is, we do not have sufficient evidence to say that the fuel treatment affects mpg.
