Table of Contents
The Chi-Square Distribution Table is used to calculate the probability of obtaining a given chi-square statistic. The table contains a set of chi-square values (along the top row) and the corresponding probability values (down the left column). To use the table, locate the chi-square value closest to the one calculated from an experiment. The probability value in the same row and column is the probability of obtaining that chi-square value.
This tutorial explains how to read and interpret .
What is the Chi-Square Distribution Table?
The Chi-Square distribution table is a table that shows the critical values of the Chi-Square distribution. To use the Chi-Square distribution table, you only need to know two values:
- The degrees of freedom for the Chi-Square test
- The alpha level for the test (common choices are 0.01, 0.05, and 0.10)
The following image shows the first 20 rows of the Chi-Square distribution table, with the degrees of freedom along the left side of the table and the alpha levels along the top of the table:
Note: You can find a full Chi-Square distribution table with more degrees of freedom .
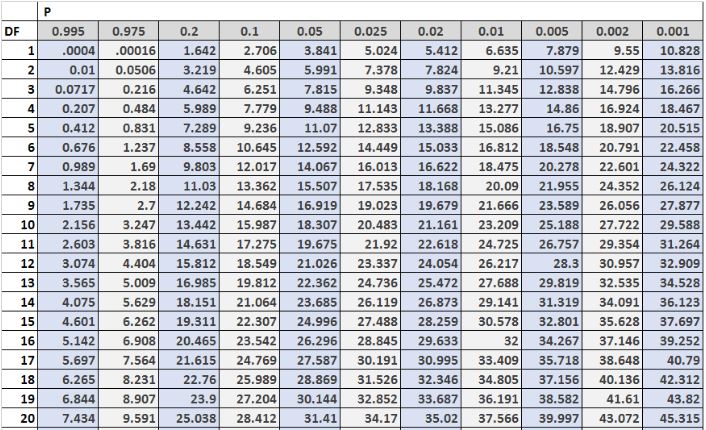
The critical values within the table are often compared to the test statistic of a Chi-Square test. If the test statistic is greater than the critical value found in the table, then you can reject the null hypothesis of the Chi-Square test and conclude that the results of the test are statistically significant.
Examples of How to Use the Chi-Square Distribution Table
We will demonstrate how to use the Chi-Square distribution table with the following three types of Chi-Square tests:
- Chi-Square Test for Independence
- Chi-Square Test for Goodness of Fit
- Chi-Square Test for Homogeneity
Chi-Square Test for Independence
We use a Chi-Square test for independence when we want to test whether or not there is a significant association between two categorical variables.
Example: Suppose we want to know whether or not gender is associated with political party preference. We take a simple random sample of 500 voters and survey them on their political party preference. Using a 0.05 level of significance, we conduct a chi-square test for independence to determine if gender is associated with political party preference. The following table shows the results of the survey:

It turns out that the test statistic for this Chi-Square test is 0.864.
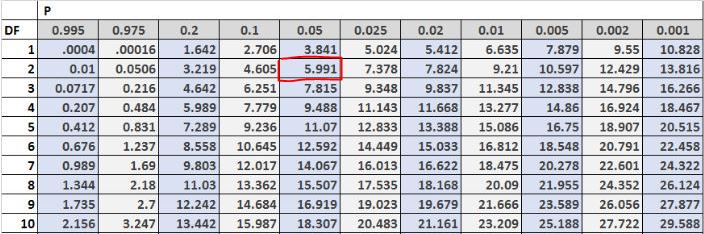
Next, we can find the critical value for the test in the Chi-Square distribution table. The degrees of freedom is equal to (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 and the problem told us that we are to use a 0.05 alpha level. Thus, according to the Chi-Square distribution table, the critical value of the test is 5.991.
Chi-Square Test for Goodness of Fit
We use a chi-square goodness of fit test when we want to test whether or not a categorical variable follows a hypothesized distribution.
Example: An owner of a shop claims that 30% of all his weekend customers visit on Friday, 50% on Saturday, and 20% on Sunday. An independent researcher visits the shop on a random weekend and finds that 91 customers visit on Friday, 104 visit on Saturday, and 65 visit on Sunday. Using a 0.10 level of significance, we conduct a chi-square test for goodness of fit to determine if the data is consistent with the shop owner’s claim.
In this case, the test statistic turns out to be 10.616.
Next, we can find the critical value for the test in the Chi-Square distribution table. The degrees of freedom is equal to (#outcomes-1) = 3-1 = 2 and the problem told us that we are to use a 0.10 alpha level. Thus, according to the Chi-Square distribution table, the critical value of the test is 4.605.

Since our test statistic is greater than our critical value, we reject the null hypothesis. This means we have sufficient evidence to say the true distribution of customers who come in to this shop on weekends is not equal to 30% on Friday, 50% on Saturday, and 20% on Sunday.
Chi-Square Test for Homogeneity
We use a chi-square test for homogeneity when we want to formally test whether or not there is a difference in proportions between several groups.
Example:A basketball training facility wants to see if two new training programs improve the proportion of their players who pass a difficult shooting test. 172 players are randomly assigned to program 1, 173 to program 2, and 215 to the current program. After using the training programs for one month, the players then take a shooting test. The table below shows the number of players who pass the shooting test, based on which program they used.

Using a 0.05 level of significance, we conduct a chi-square test for homogeneity to determine if the pass rate is the same or each training program.
It turns out that the test statistic for this Chi-Square test is 4.208.
Next, we can find the critical value for the test in the Chi-Square distribution table. The degrees of freedom is equal to (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 and the problem told us that we are to use a 0.05 alpha level. Thus, according to the Chi-Square distribution table, the critical value of the test is 5.991.

Since our test statistic is smaller than our critical value, we fail to reject the null hypothesis. This means we do not have sufficient evidence to say that the three training programs produce different results.
