Table of Contents
The Binomial Distribution Table is used to calculate the probability of a binomial random variable. The table gives the cumulative probability of different outcomes for a given number of trials and probability of success. It can be read by finding the given number of trials across the top row and the probability of success down the left-hand column. The number at the intersection is the cumulative probability of that number of successes or fewer out of the given number of trials.
The binomial distribution table is a table that shows probabilities associated with the . To use the binomial distribution table, you only need three values:
- n: the number of trials
- r: the number of “successes” during n trials
- p: the probability of success on a given trial
Using these three numbers, you can use the binomial distribution table to find the probability of obtaining exactly r successes during n trials when the probability of success on each trial is p.
The following examples illustrate how to read the binomial distribution table.
Example 1
Question: Jessica makes 60% of her free-throw attempts. If she shoots 6 free throws, what is the probability that she makes exactly 4?
To answer this question, we can look up the value in the binomial distribution table that corresponds to n = 6, r = 4, and p = 0.60:
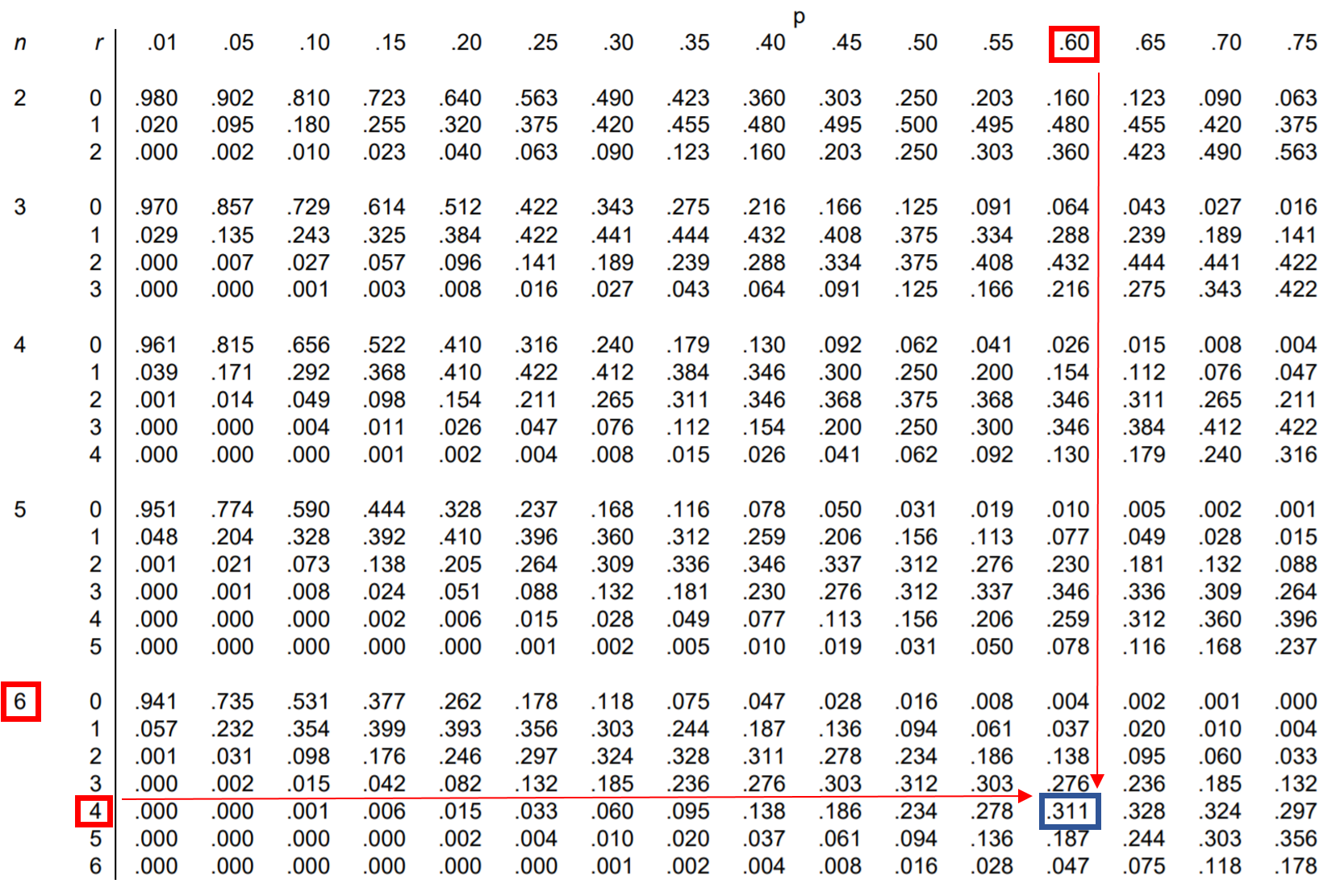
The probability that Jessica makes exactly 4 out of 6 free throws is 0.311.
Example 2
Question: Jessica makes 60% of her free-throw attempts. If she shoots 6 free throws, what is the probability that she makes less than 4?
To find this probability, we actually have to add up the following probabilities:
P(makes less than 4) = P(makes 0) + P(makes 1) + P(makes 2) + P(makes 3)
So, we can look up each of these four probabilities in the binomial distribution table and add them up:
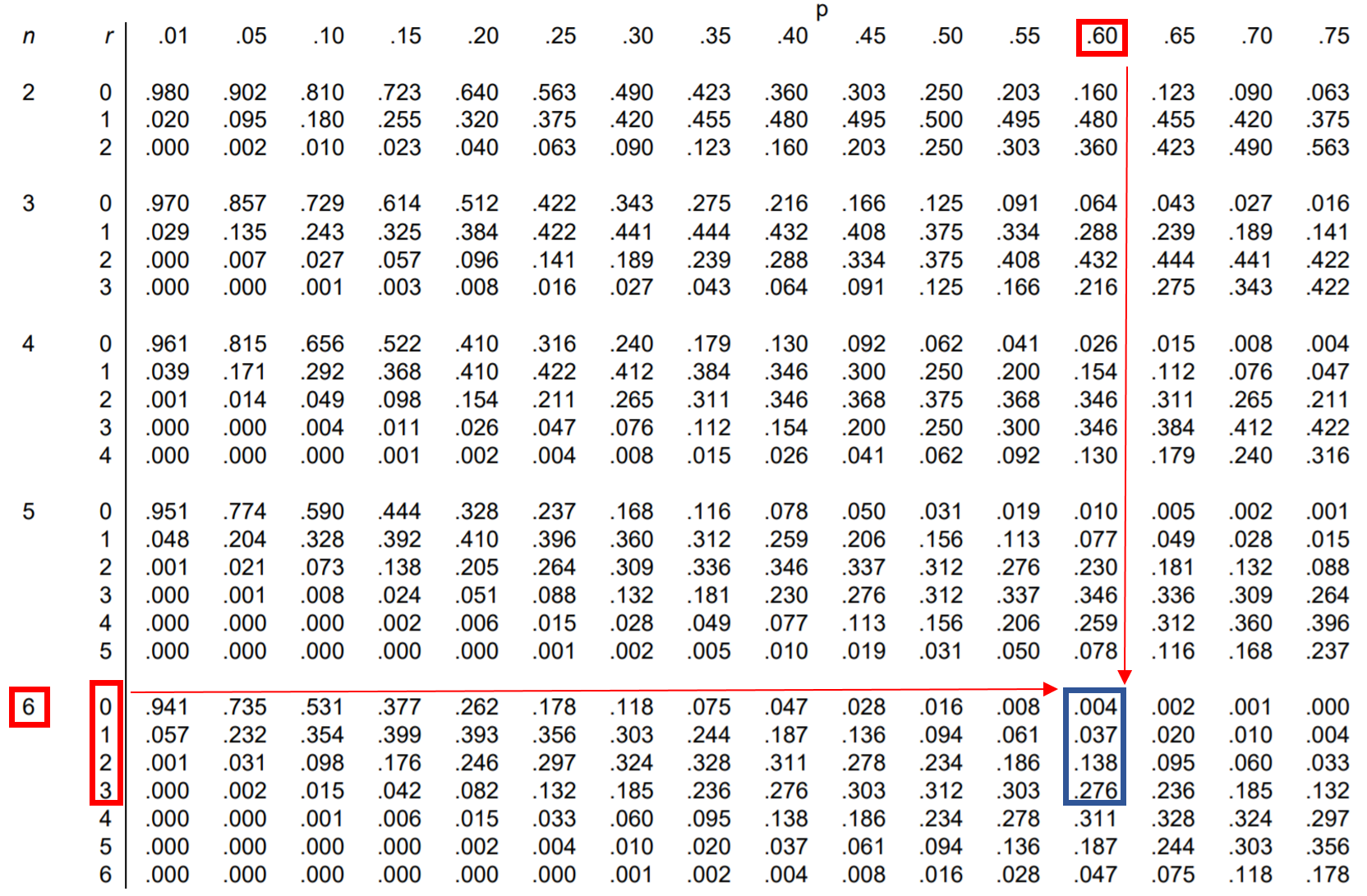
According to the table, P(makes less than 4) = .004 + .037 + .138 + .276 = 0.455.
The probability that Jessica makes less than 4 free throws is 0.455.
Example 3
Question: Jessica makes 60% of her free-throw attempts. If she shoots 6 free throws, what is the probability that she makes 4 or more?
To find this probability, we have to add up the following probabilities:
P(makes 4 or more) = P(makes 4) + P(makes 5) + P(makes 6)
So, we can look up each of these three probabilities in the binomial distribution table and add them up:
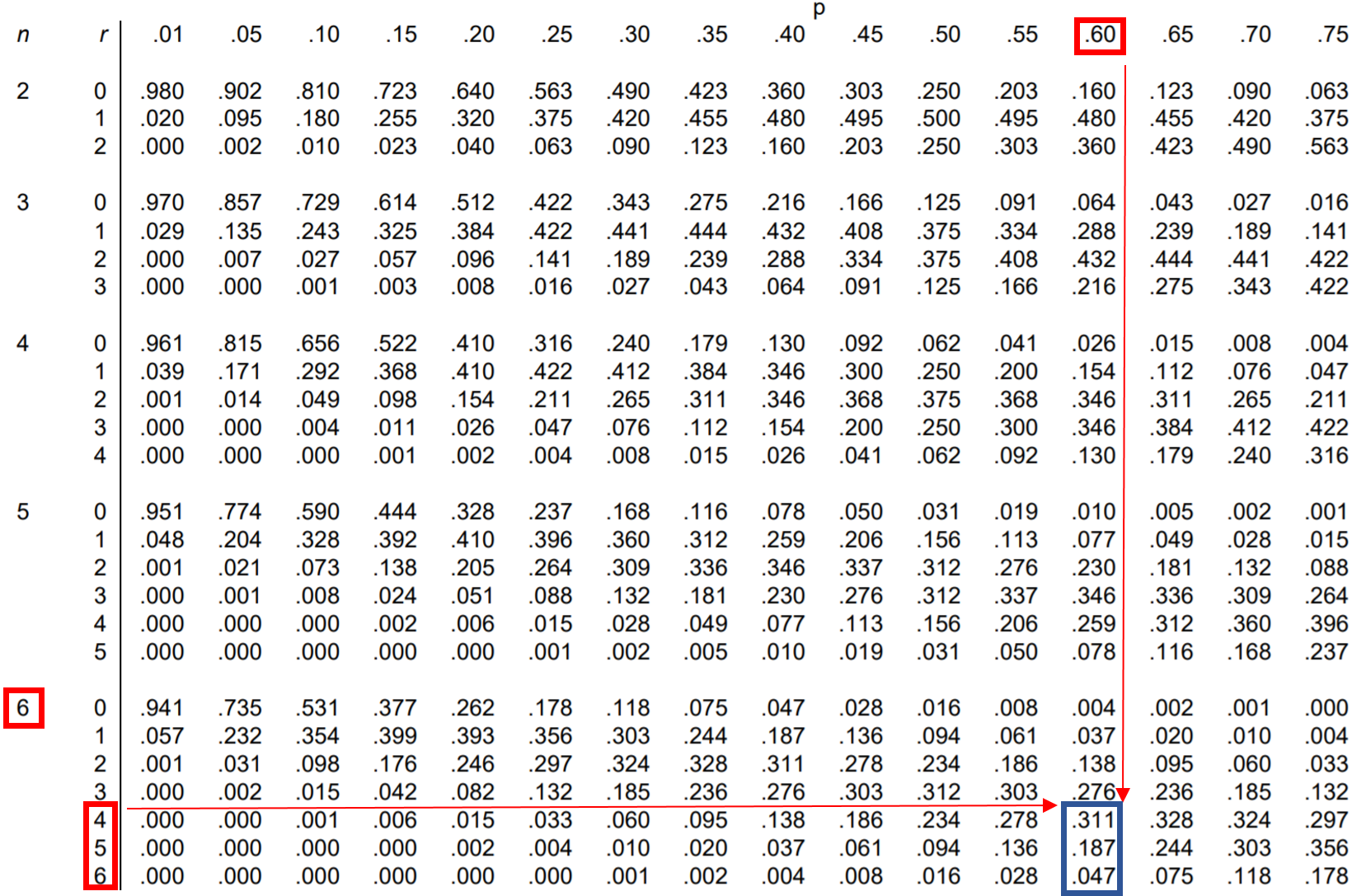
According to the table, P(makes 4 or more) = .311 + .187 + .047 = 0.545.
The probability that Jessica makes 4 or more free throws is 0.545.
