Table of Contents
Chi-Square Test is a statistical test used to determine if there is a significant association between two categorical variables. In SPSS, the results of this test can be interpreted by looking at the Chi-Square value and the p-value. The Chi-Square value measures the overall difference between the observed and expected frequencies, while the p-value indicates the probability of obtaining such a difference by chance. If the p-value is less than the chosen significance level (usually 0.05), then there is evidence of a significant association between the variables. On the other hand, if the p-value is greater than the significance level, there is no significant association. Additionally, examining the standardized residuals can provide information about which specific categories are contributing to the overall Chi-Square value.
A is used to determine whether or not there is a significant association between two categorical variables.
The following example shows how to interpret the results of a Chi-Square test of Independence in SPSS.
Example: How to Interpret Chi-Square Test of Independence Results in SPSS
Suppose we want to know whether or not gender is associated with political party preference.
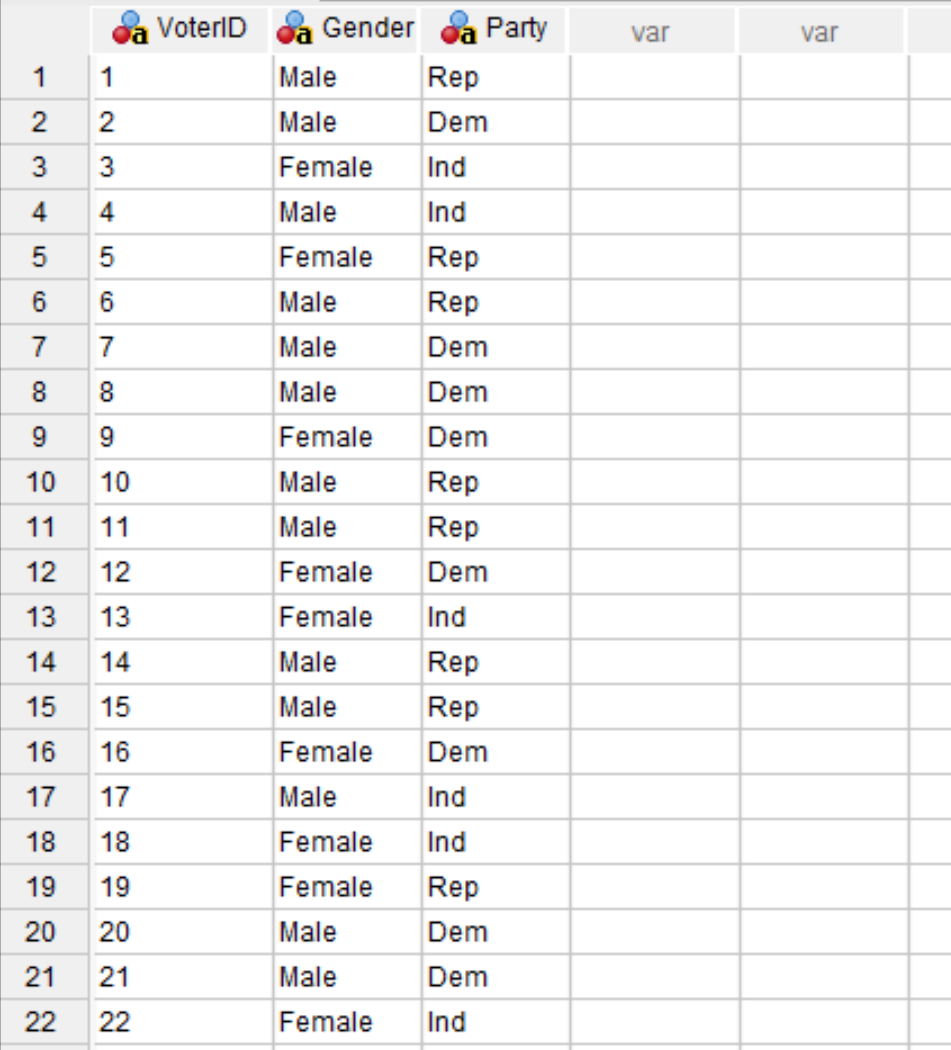
We take a simple random sample of 50 voters and survey them on their political party preference.
The following screenshot shows how to enter this data into SPSS:
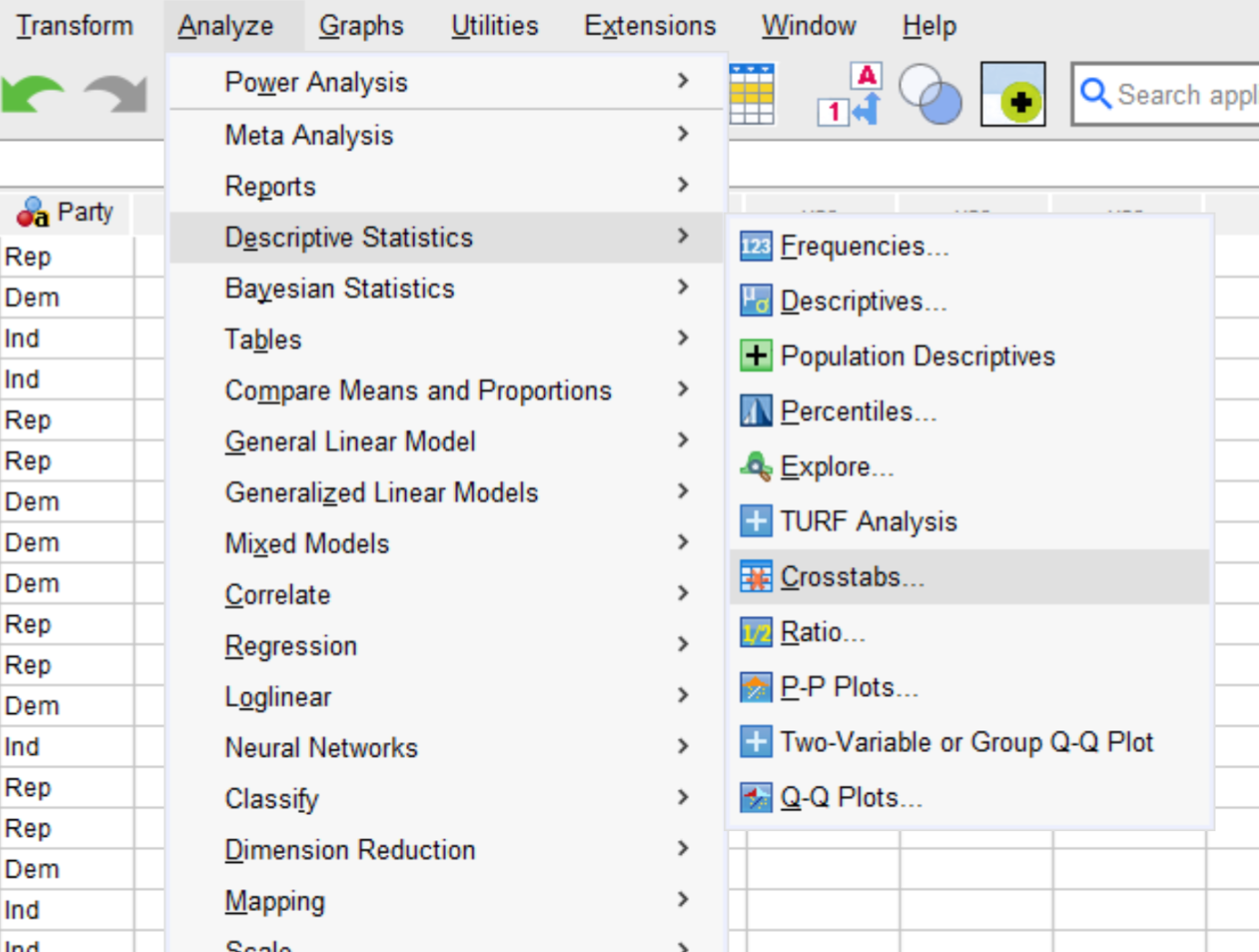
To perform a Chi-Square test of Independence, click the Analyze tab, then click Descriptive Statistics, then click Crosstabs:
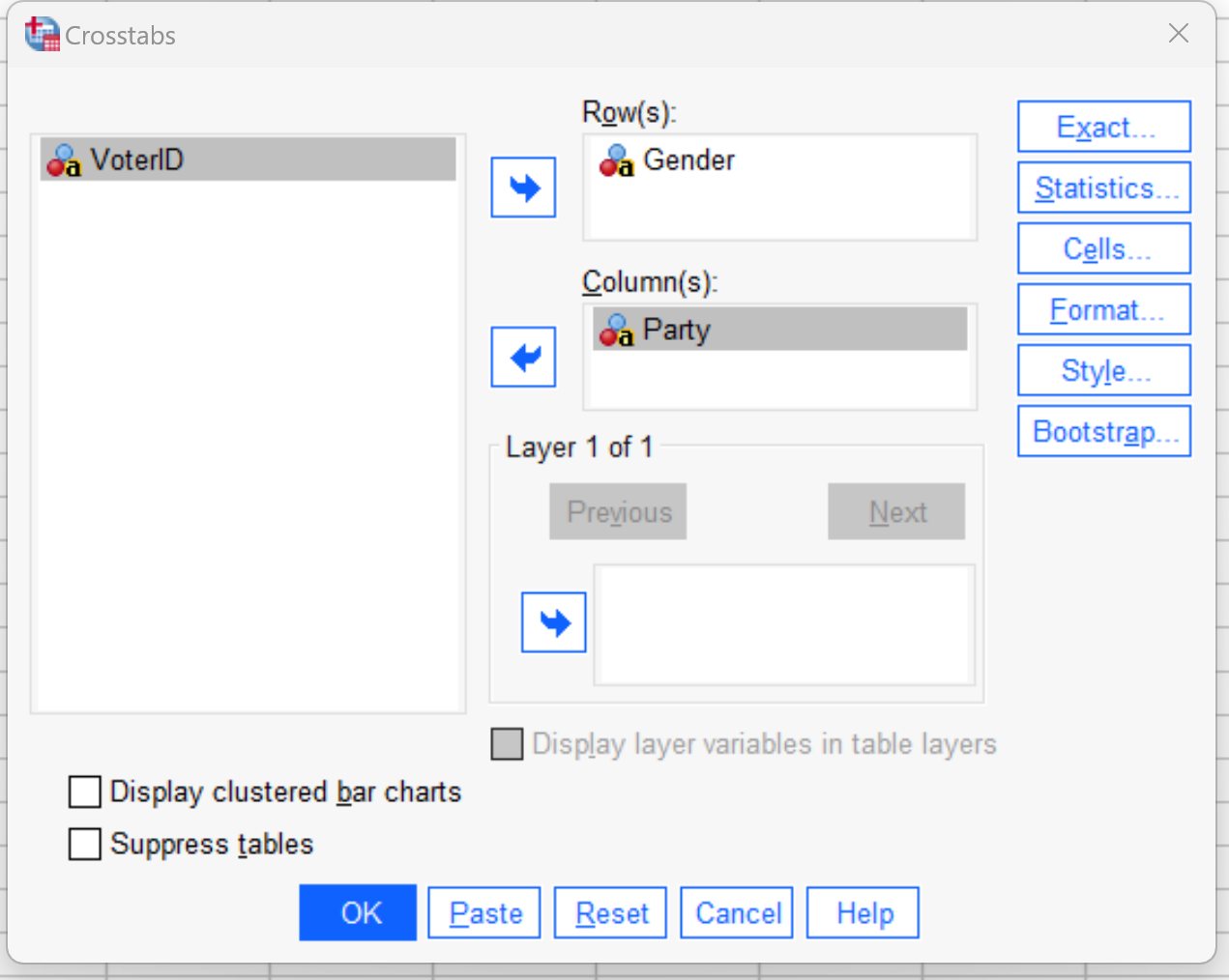
In the new window that appears, drag Gender into the Rows panel, then drag Party into the Columns panel:
Next, click the Cells button. Then check the boxes next to Observed and Expected:
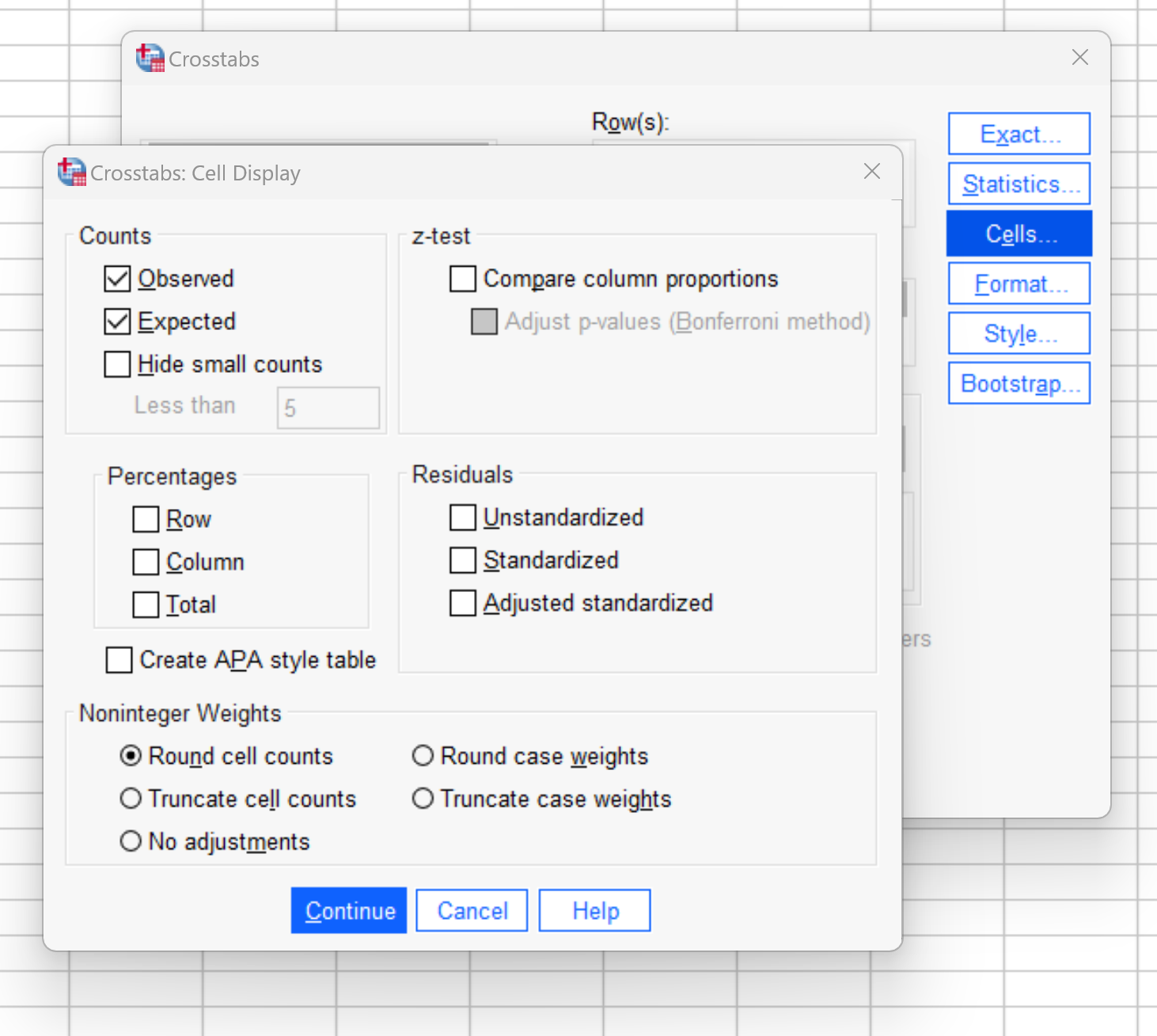
Then click Continue.
Next, click the Statistics button. Then check the box next to Chi-square:
Then click Continue.
Then click OK.
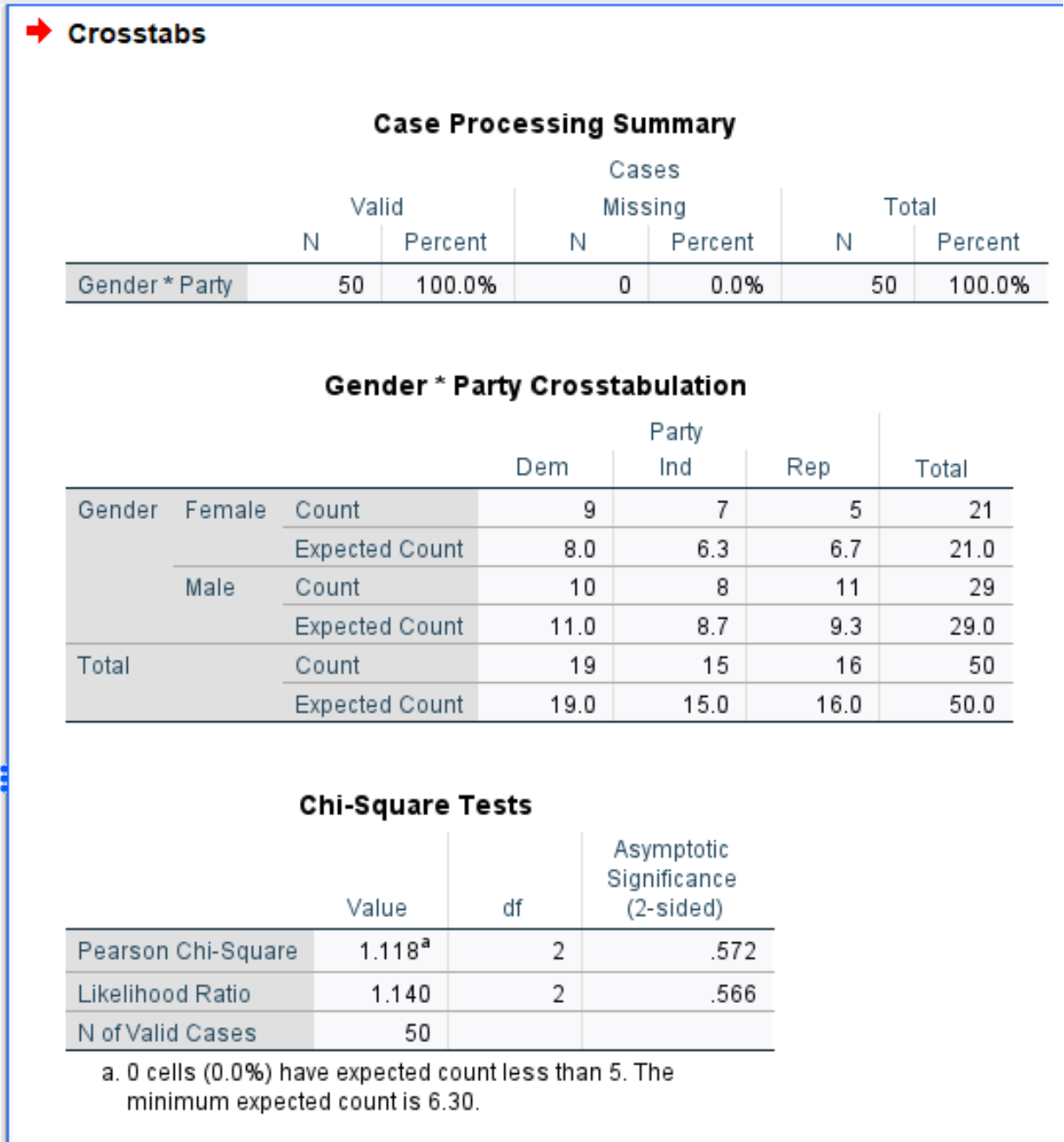
Case Processing Summary
This table displays the number of valid observations and missing observations in the dataset.
We can see that there are 50 valid observations and 0 missing observations.
Crosstabulation
This table displays a crosstab of the total number of individuals by gender and political party preference, including the observed count for each group and the expected count.
Refer to for an explanation of how to calculate expected counts in a Chi-Square test.
Chi-Square Tests
This table shows the results of the Chi-Square Test of Independence.
The Chi-Square test statistic is 1.118 and the corresponding two-sided p-value is .572.
Recall the hypotheses used for a Chi-Square Test of Independence:
- H0: The two variables are independent.
- HA: The two variables are not independent, i.e. they are associated.
In this particular example, our null hypothesis is that gender and political party preference are independent.
Since the p-value (.572) of the test is not less than 0.05, we fail to reject the null hypothesis.
Thus, we do not have sufficient evidence to say that there is an association between gender and political party preference.
Additional Resources
The following tutorials explain how to perform other common tasks in SPSS:
