Table of Contents
A probability distribution table is a chart which shows the probability of a certain outcome occurring for a particular event. It typically shows the probability of each possible outcome, as well as the cumulative probability of all the outcomes combined. It is commonly used to understand how likely an event is to happen, and can be used to make decisions about ways to minimize risks or maximize rewards.
A probability distribution table is a table that displays the probability that a takes on certain values.
For example, the following probability distribution table tells us the probability that a certain soccer team scores a certain number of goals in a given game:
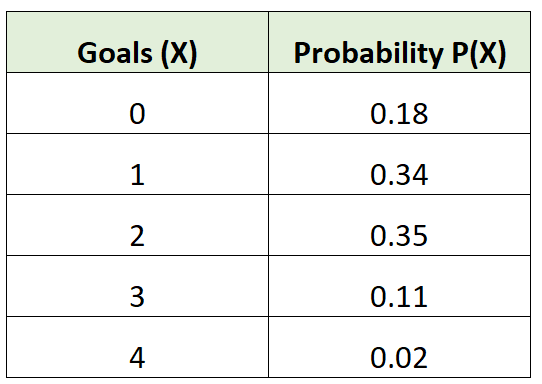
The left-hand column shows the number of goals and the right-hand column tells us the probability that the team will score this number of goals.
For example:
- The probability that the team scores exactly 0 goals is 0.18.
- The probability that the team scores exactly 1 goal is 0.34.
- The probability that the team scores exactly 2 goals is 0.35.
And so on.
Properties of a Probability Distribution Table
A probability distribution table has the following properties:
1. All probabilities must add up to 1.
For a probability distribution table to be valid, all of the individual probabilities must add up to 1. We can verify that the previous probability distribution table is valid:
Sum of probabilities = 0.18 + 0.34 + 0.35 + 0.11 + 0.02 = 1.
2. The mean can be calculated.
The formula to calculate the mean of a given probability distribution table is:
μ = Σx * P(x)
where:
- x: Data value
- P(x): Probability of value

The mean number of goals for the soccer team would be calculated as:
μ = 0*0.18 + 1*0.34 + 2*0.35 + 3*0.11 + 4*0.02 = 1.45 goals.
3. The standard deviation can be calculated.
The formula to calculate the standard deviation of a given probability distribution table is:
σ = √Σ(xi-μ)2 * P(xi)
where:
- xi: The ith value
- μ: The mean of the distribution
- P(xi): The probability of the ith value
For example, here’s how to calculate the standard deviation of goals scored by the soccer team:
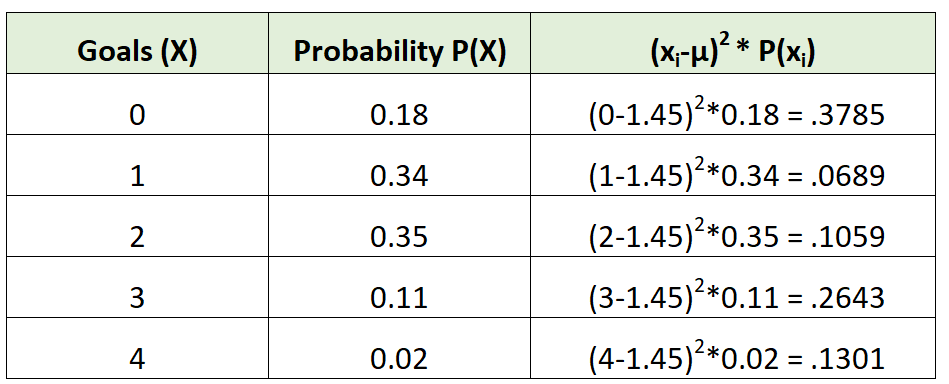
The standard deviation is the square root of the sum of the values in the third column:
Standard deviation = √(.3785 + .0689 + .1059 + .2643 + .1301) = 0.9734
How to Visualize a Probability Distribution Table
The easiest way to visualize the values in a probability distribution table is by using a histogram, which displays the values of the random variable along the x-axis and the probability of those values along the y-axis:

This lets us quickly visualize the probability values from the table.
In particular, we can see that there is a high probability that the team scores 2 goals or less while there is a tiny probability that the team scores as many as 4 goals.
