Table of Contents
The Phi Coefficient, also known as the Pearson’s correlation coefficient, is a measure of the relationship between two categorical variables. It determines the extent to which two variables are associated, and can range from -1 to +1. A positive value indicates a positive correlation, while a negative value indicates a negative correlation. A value of 0 indicates no correlation between the variables.
The Phi Coefficient is commonly used in statistical analysis to determine the strength and direction of the relationship between two categorical variables. For example, it can be used to assess the relationship between gender and voting preferences, or between education level and job satisfaction.
Furthermore, the Phi Coefficient is also used in research studies to determine the effectiveness of a particular intervention or treatment. For instance, it can be used to measure the impact of a new teaching method on students’ academic performance.
Overall, the Phi Coefficient is a useful tool in understanding and analyzing the relationship between categorical variables and is widely used in various fields such as psychology, sociology, and marketing.
Phi Coefficient: Definition & Examples
A Phi Coefficient (sometimes called a mean square contingency coefficient) is a measure of the association between two binary variables.
For a given 2×2 table for two random variables x and y:

The Phi Coefficient can be calculated as:
Φ = (AD-BC) / √(A+B)(C+D)(A+C)(B+D)
Example: Calculating a Phi Coefficient
Suppose we want to know whether or not gender is associated with political party preference. We take a simple random sample of 25 voters and survey them on their political party preference. The following table shows the results of the survey:
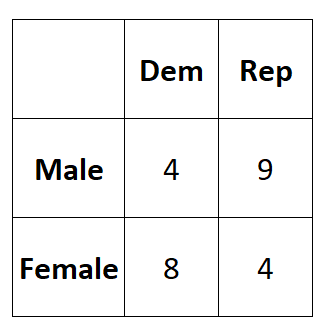
We can calculate the Phi Coefficient between the two variables as:
Φ = (4*4-9*8) / √(4+9)(8+4)(4+8)(9+4) = (16-72) / √24336 = -0.3589
Note: We could have also calculated this using the Phi Coefficient Calculator.
How to Interpret a Phi Coefficient
Similar to a Pearson Correlation Coefficient, a Phi Coefficient takes on values between -1 and 1 where:
- -1 indicates a perfectly negative relationship between the two variables.
- 0 indicates no association between the two variables.
- 1 indicates a perfectly positive relationship between the two variables.
In general, the further away a Phi Coefficient is from zero, the stronger the relationship between the two variables.
In other words, the further away a Phi Coefficient is from zero, the more evidence there is for some type of systematic pattern between the two variables.
Additional Resources
A Guide to the Pearson Correlation Coefficient
A Guide to Fisher’s Exact Test
A Guide to the Chi-Square Test of Independence
