# How to Calculate a Phi Coefficient in R

---

A Phi Coefficient (sometimes called a mean square contingency coefficient) is a measure of the association between two binary variables.

For a given 2×2 table for two random variables x and y:

The Phi Coefficient can be calculated as:

Φ = (AD-BC) / √(A+B)(C+D)(A+C)(B+D)

Example: Calculating a Phi Coefficient in R

Suppose we want to know whether or not gender is associated with political party preference so we take a of 25 voters and survey them on their political party preference.

The following table shows the results of the survey:

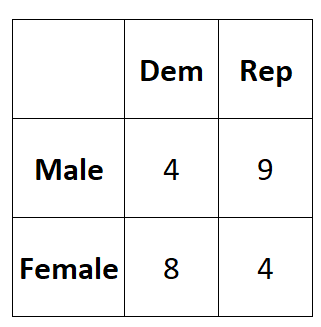
We can use the following code to enter this data into a 2×2 matrix in R:

#create 2x2 table
data = matrix(c(4, 8, 9, 4), nrow = 2)

#view dataset
data

     [,1] [,2]
[1,]    4    9
[2,]    8    4

We can then use the function from the psych package to calculate the Phi Coefficient between the two variables:

#load psych package
library(psych)

#calculate Phi Coefficient
phi(data)

[1] -0.36

The Phi Coefficient turns out to be -0.36.

Note that the phi function rounds to 2 digits by default, but you can specify the function to round to as many digits as you’d like:

#calculate Phi Coefficient and round to 6 digits
phi(data, digits = 6)

[1] -0.358974

How to Interpret a Phi Coefficient

• -1 indicates a perfectly negative relationship between the two variables.
• 0 indicates no association between the two variables.
• 1 indicates a perfectly positive relationship between the two variables.

In general, the further away a Phi Coefficient is from zero, the stronger the relationship between the two variables.

In other words, the further away a Phi Coefficient is from zero, the more evidence there is for some type of systematic pattern between the two variables.