Table of Contents
A high F value in ANOVA indicates a significant difference between the means of different groups, indicating that there is a statistically significant difference between the means of the groups compared. This means that the observed variance between the groups is likely due to the independant variable and not due to random chance.
A is used to determine whether or not the means of three or more independent groups are equal.
A one-way ANOVA uses the following null and alternative hypotheses:
- H0: All group means are equal.
- HA: At least one group mean is different from the rest.
Whenever you perform a one-way ANOVA, you will end up with a summary table that looks like the following:
| Source | Sum of Squares (SS) | df | Mean Squares (MS) | F | P-value |
|---|---|---|---|---|---|
| Treatment | 192.2 | 2 | 96.1 | 2.358 | 0.1138 |
| Error | 1100.6 | 27 | 40.8 | ||
| Total | 1292.8 | 29 |
The F-value in the table is calculated as:
- F-value = Mean Squares Treatment / Mean Squares Error
Another way to write this is as follows:
- F-value = variation between sample means / variation within the samples
If the variation between the sample means is high relative to the variation within each of the samples, then the F-value will be large.
For example, the F-value in the table above is calculated as:
- F-value = 96.1 / 40.8 = 2.358
To find the that corresponds to this F-value, we can use an with numerator degrees of freedom = df Treatment and denominator degrees of freedom = df Error.
For example, the p-value that corresponds to an F-value of 2.358, numerator df = 2, and denominator df = 27 is 0.1138.
Since this p-value is not less than α = .05, we fail to reject the null hypothesis. This means there is no statistically significant difference between the means of the three groups.
Visualizing the F-Value of an ANOVA
To gain an intuitive understanding of the F-value in an ANOVA table, consider the following example.
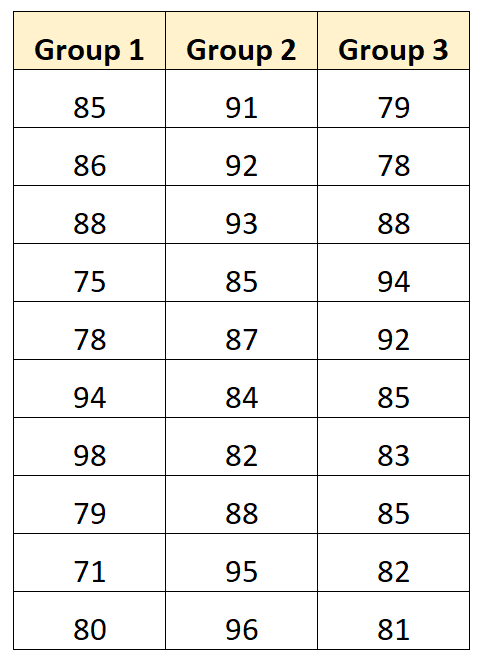
We can create the following plot to visualize the exam scores by group:
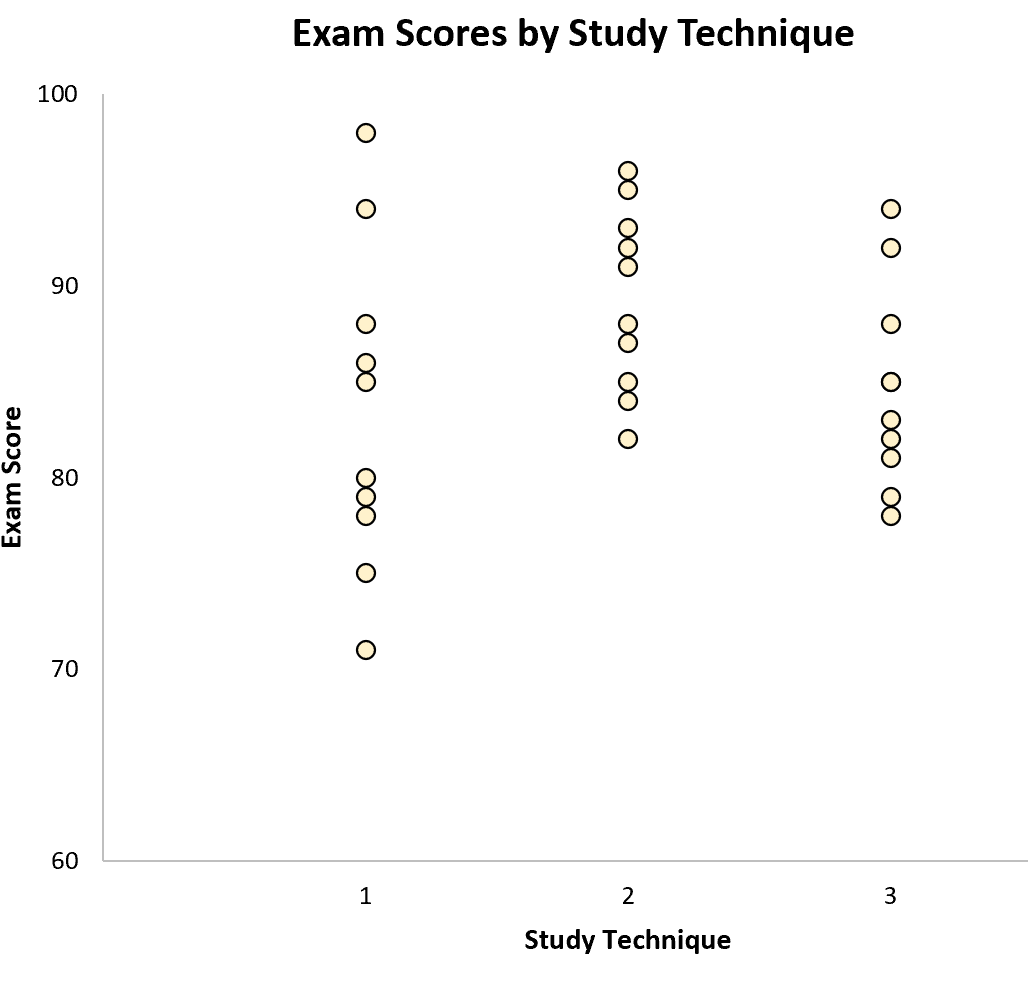
The variation within the samples is represented by the spread of the values within each individual sample:
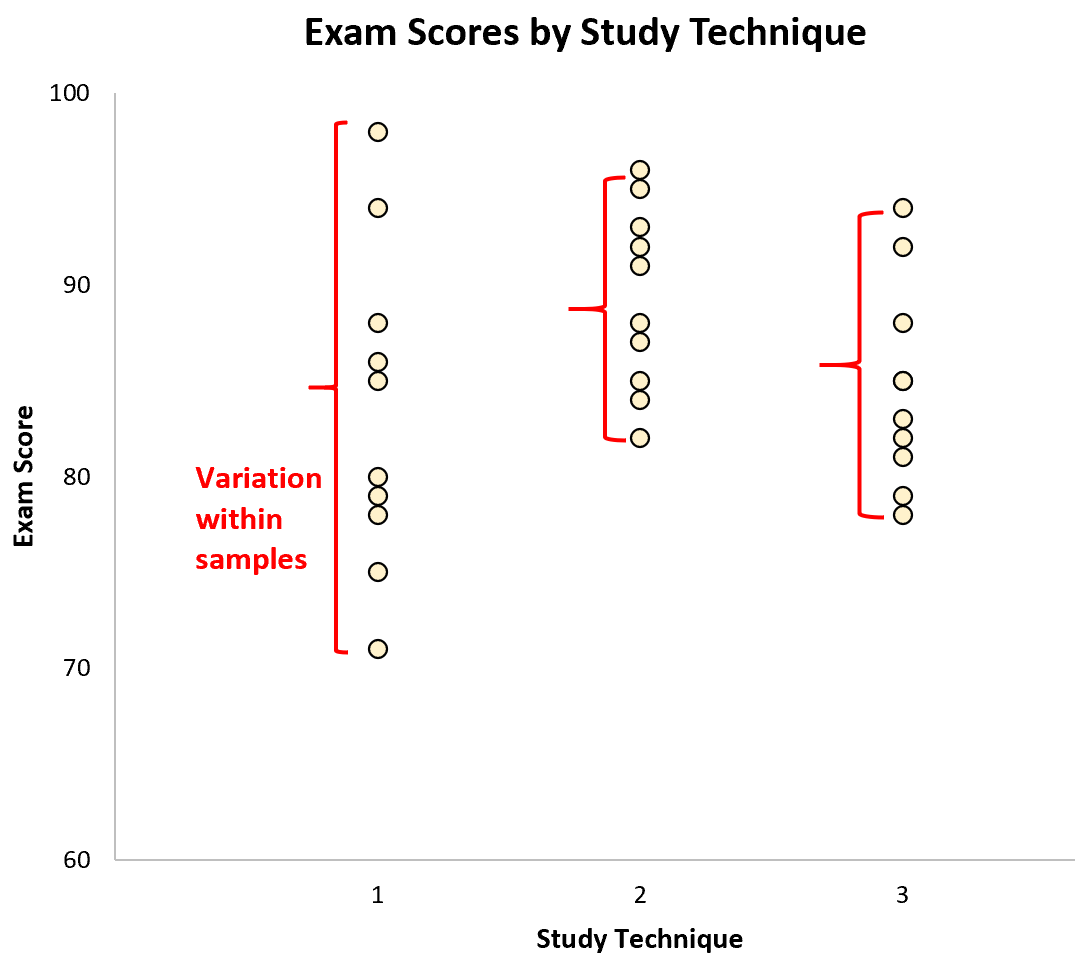
The variation between the samples is represented by the differences between the sample means:
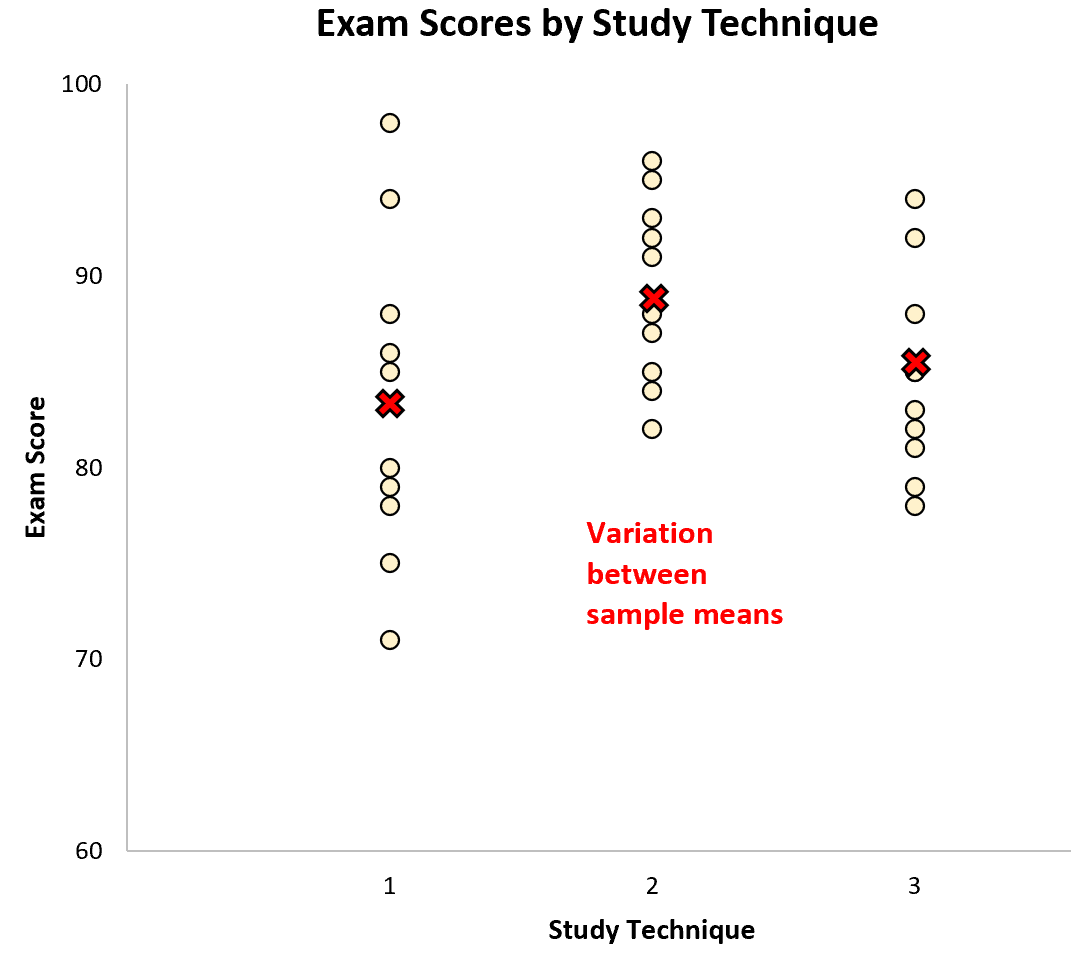
Upon performing a one-way ANOVA for this dataset, we find that the F-value is 2.358 and the corresponding p-value is 0.1138.
Since this p-value is not less than .05, we fail to reject the null hypothesis. This means we don’t have sufficient evidence to say that the studying technique used causes statistically significant differences in mean exam scores.
In other words, this tells us that the variation between the sample means is not high enough relative to the variation within the samples to reject the null hypothesis.
Conclusion
Here’s a brief summary of the main points in this article:
- The F-value in an ANOVA is calculated as: variation between sample means / variation within the samples.
- The higher the F-value in an ANOVA, the higher the variation between sample means relative to the variation within the samples.
- The higher the F-value, the lower the corresponding p-value.
- If the p-value is below a certain threshold (e.g. α = .05), we can reject the null hypothesis of the ANOVA and conclude that there is a statistically significant difference between group means.
