Table of Contents
One-Way ANOVA is a statistical test used to compare the means of three or more groups of data, while Repeated Measures ANOVA is a statistical test used to compare the means of multiple measurements of the same group of individuals. The difference between the two is that with One-Way ANOVA, each group is of a different population, while with Repeated Measures ANOVA, the same population is measured multiple times.
Two types of ANOVA models that students often get confused between are the one-way ANOVA and the repeated measures one-way ANOVA.
Here’s the simple difference:
A one-way ANOVA is used to determine whether or not there is a statistically significant difference between the means of three or more independent groups.
A repeated measures one-way ANOVA is used to determine whether or not there is a statistically significant difference between the means of three or more groups in which the same subjects show up in each group.
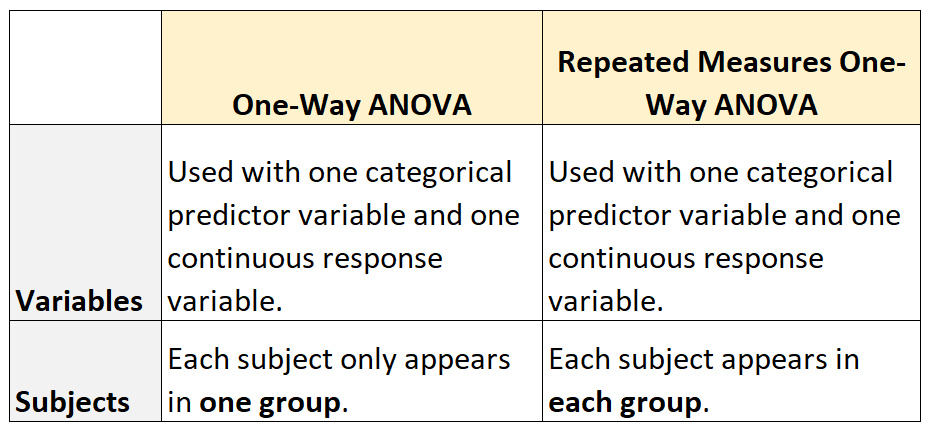
For example, suppose a professor wants to determine if three different studying techniques lead to different mean exam scores. To test this, he recruits 15 students and randomly assigns 5 students to use each studying technique for one week before the exam.
He could use a one-way ANOVA to test for differences between the group means since each student only appears in one group each.
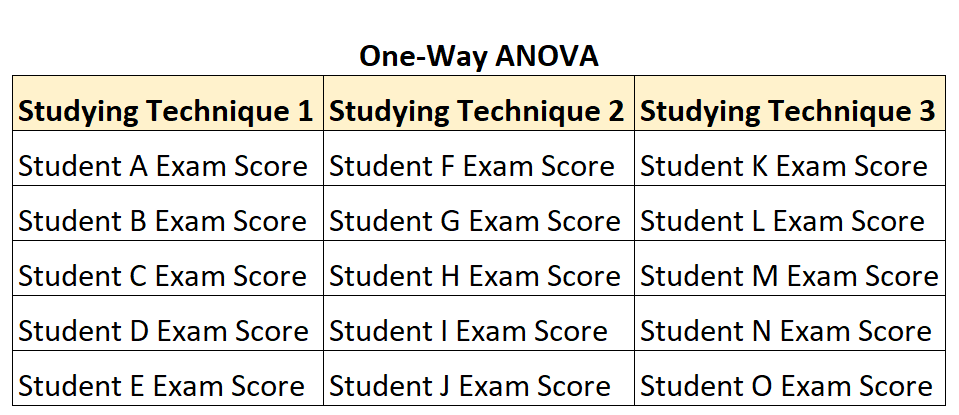
However, suppose the professor recruits just 5 students and has each student use each studying technique during three different weeks to prepare for tests of equal difficulty.
In this scenario, he could use a repeated measures one-way ANOVA to test for differences between the group means since each student appears in each group.

When to Use a Repeated Measures ANOVA
A repeated measures ANOVA is used in two specific situations:
1. Measuring the mean scores of subjects during three or more time points. For example, you might want to measure the resting heart rate of subjects one month before they start a training program, once during the middle of the program, and one month after the program to see if there is a significant difference in mean resting heart rate across these three time points.
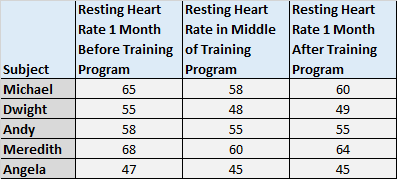
Since the heart rate of each subject is measured repeatedly, we can use a repeated measures ANOVA to determine if there is a significant difference in mean heart rate across these three time periods.
2. Measuring the mean scores of subjects under three different conditions. For example, you might have subjects watch three different movies and rate each one based on how much they enjoyed it.

Again, the same subjects show up in each group, so we need to use a repeated measures ANOVA to test for the difference in means across these three conditions.
Pros & Cons of the Repeated Measures ANOVA
A repeated measures one-way ANOVA offers the following pros over the ordinary one-way ANOVA:
1. It’s faster and more cost-effective to recruit a small number of individuals to participate in a repeated measures one-way ANOVA since researchers can simply obtain data from the same individuals multiple times.
2. Researchers can attribute a portion of the variance in the data to the individuals themselves, which makes it easier to detect true differences that exist between the different treatments.
However, a repeated measures one-way ANOVA comes with the following cons:
1. If one individual drops out of the experiment, researchers lose out on more data compared to an ordinary one-way ANOVA.
2. There is the potential for individuals to suffer from – which refers to differences in participant behavior as a result of the order in which treatments are presented to them. For example, individuals may become tired or fatigued by time they experience the last treatment.
