Table of Contents
Performing a correlation test in SPSS involves first importing your data into the software and selecting the variables you want to test. Then, you would choose the appropriate correlation test (such as Pearson’s correlation or Spearman’s rank correlation) based on the type of data you have. The software will then calculate the correlation coefficient and provide a significance value to determine if the relationship between the variables is statistically significant. The results can be interpreted to determine the strength and direction of the relationship between the variables.
In statistics, we often use the Pearson correlation coefficient to measure the linear association between two variables.
To determine if a correlation coefficient is statistically significant, we can perform a correlation test in which we calculate a t-score and corresponding p-value.
A correlation test uses the following hypotheses:
- H0: The correlation between the two variables is not statistically significant.
- HA: The correlation between the two variables is statistically significant.
If the p-value of the test is less than some significance level (e.g. α = .05) then we can reject the null hypothesis and conclude that the correlation between the two variables is statistically significant.
The easiest way to perform a correlation test in SPSS is by using Analyze > Correlate > Bivariate.
The following example shows how to do so in practice.
Example: How to Perform a Correlation Test in SPSS
Suppose we have the following two variables in SPSS named X and Y:
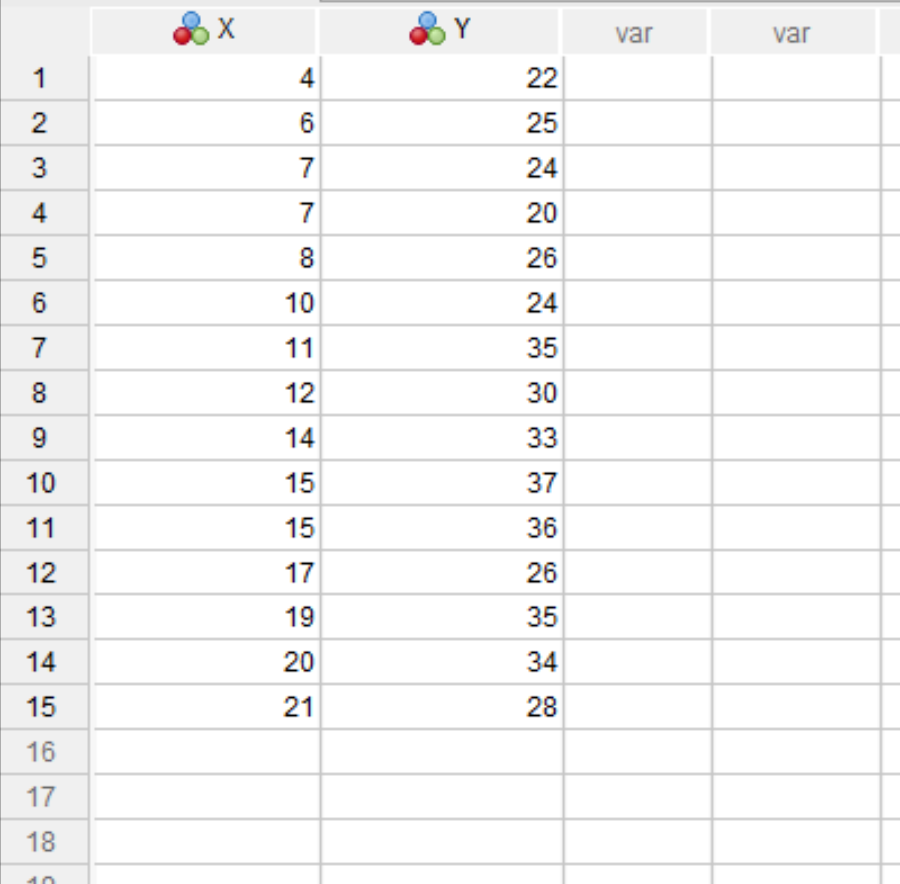
Suppose that we would like to calculate the correlation between these two variables and perform a correlation test to determine if the correlation coefficient is statistically significant.
To do so, click the Analyze tab, then click Correlate, then click Bivariate:

In the new window that appears, drag both the X and Y variables into the Variables box:
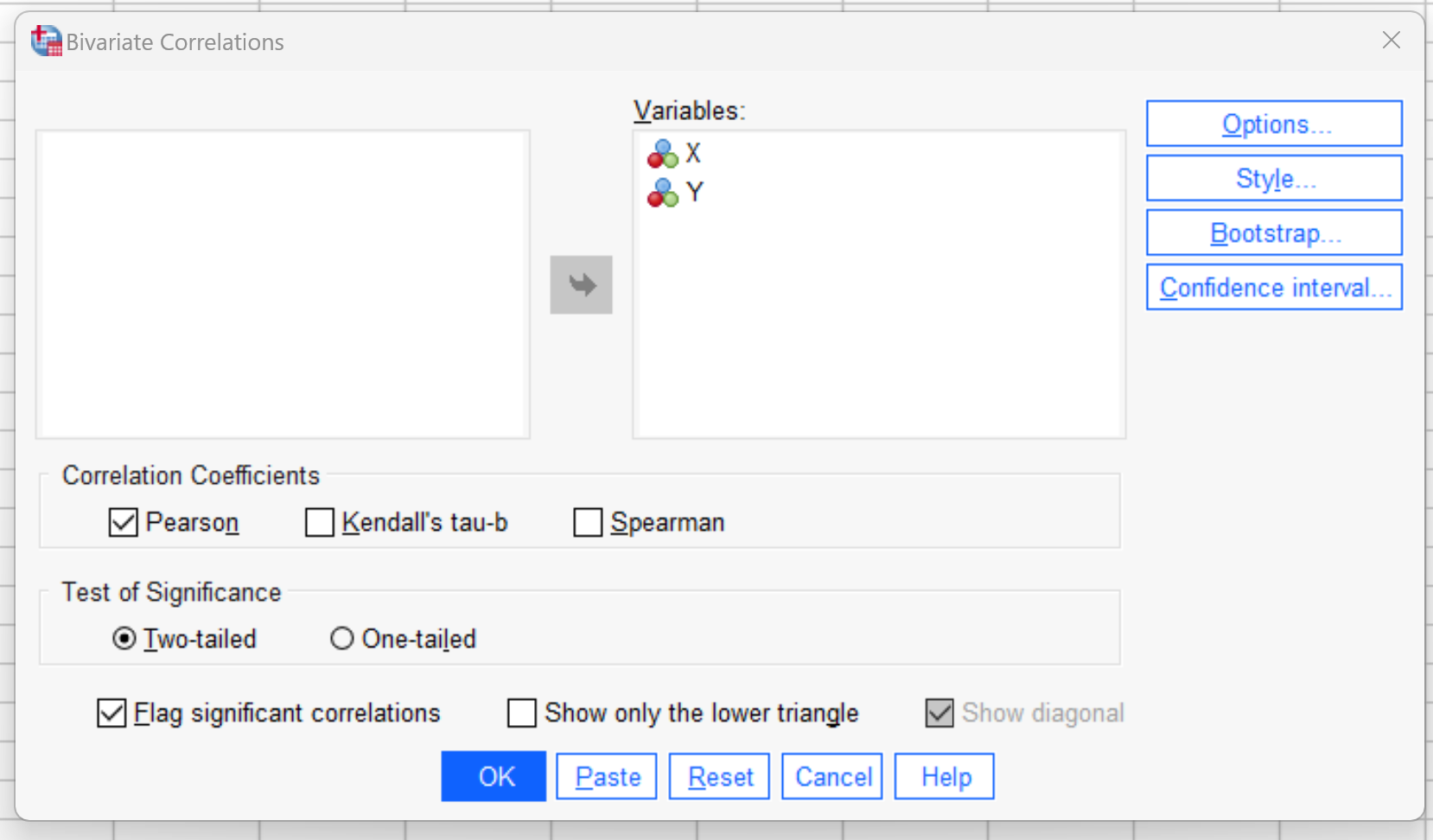
Make sure that the box is checked next to Pearson under the list of Correlation Coefficients.
Then click OK.
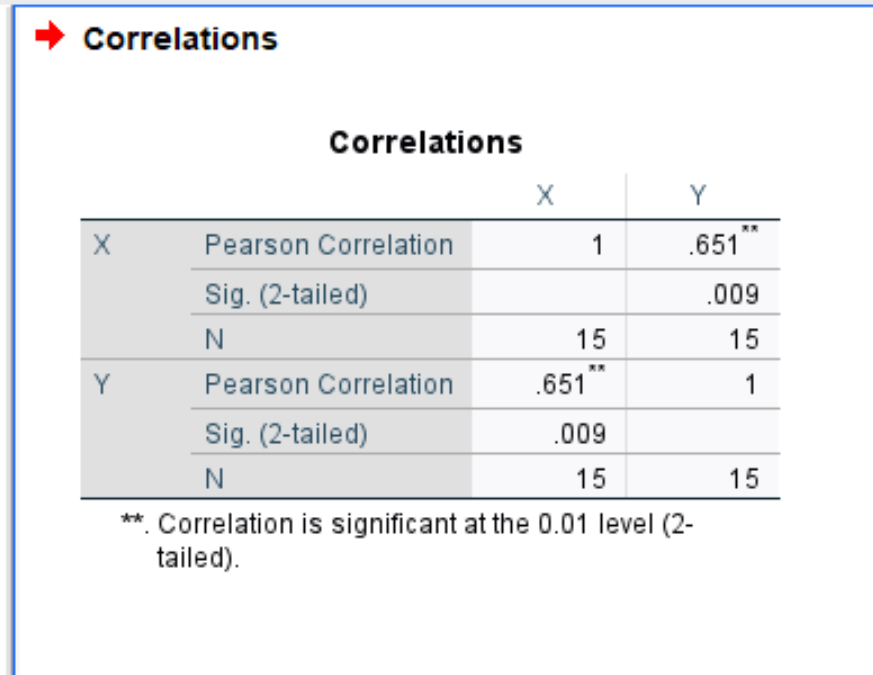
The output shows a correlation matrix between X and Y.
From the output we can see the following values:
- Pearson correlation coefficient: .651
- p-value of Pearson correlation coefficient: .009
Recall the hypotheses used in a correlation test:
- H0: The correlation between the two variables is not statistically significant.
- HA: The correlation between the two variables is statistically significant.
Since the p-value in the output (.009) is less than .05, we .
We have sufficient evidence to say that the correlation between the two variables is statistically significant.
Note: Since the Pearson correlation coefficient (.651) was a positive value, this indicates that there is a positive correlation between the two variables.
Additional Resources
The following tutorials provide additional information about correlation coefficients:
