What’s the difference between the Poisson distribution and the Normal Distribution?

---

The Poisson distribution and the normal distribution are two of the most commonly used probability distributions in statistics.

This tutorial provides a quick explanation of each distribution along with two key differences between the distributions.

An Overview: The Poisson Distribution

The Poisson distribution describes the probability of obtaining k successes during a given time interval.

If a random variable X follows a Poisson distribution, then the probability that X = k successes can be found by the following formula:

P(X=k) = λ^k * e^{– λ} / k!

where:

• λ: mean number of successes that occur during a specific interval
• k: number of successes
• e: a constant equal to approximately 2.71828

For example, suppose a particular hospital experiences an average of 2 births per hour. We can use the formula above to determine the probability of experiencing 3 births in a given hour:

P(X=3) = 2³ * e^{– 2} / 3! = 0.1805

The probability of experiencing 3 births in a given hour is 0.1805.

An Overview: The Normal Distribution

The normal distribution describes the probability that a random variable takes on a value within a given interval.

The of a normal distribution can be written as:

P(X=x) = (1/σ√2π)e^{-1/2((x-μ)/σ)2}

where:

• σ: Standard deviation of the distribution
• μ: Mean of the distribution
• x: Value for the random variable

If we randomly select an otter from this population, we can use the following formula to find the probability that it weighs between 38 and 42 pounds:

P(38 < X < 42) = (1/σ√2π)e^{-1/2((42-40)/5)2} – (1/σ√2π)e^{-1/2((38-40)/5)2} = 0.3108

The probability that the randomly selected otter weighs between 38 and 42 pounds is 0.3108.

Difference #1: Discrete vs. Continuous Data

The first difference between the Poisson and normal distribution is the type of data that each probability distribution models.

A Poisson distribution is used when you’re working with discrete data that can only take on integer values equal to or greater than zero. Some examples include:

• Number of calls received per hour at a call center
• Number of customers per day at a restaurant
• Number of car accidents per month

In each scenario, the random variable can only take on a value of 0, 1, 2, 3, etc.

A normal distribution is used when you’re working with continuous data that can take on any value from negative infinity to positive infinity. Some examples include:

• Weight of a certain animal
• Height of a certain plant
• Marathon times of females
• Temperature in Celsius

In these scenarios, the random variables can take on any value like -11.3, 21.343435, 85, etc.

Difference #2: Shape of the Distributions

The second difference between the Poisson and normal distribution is the shape of the distributions.

A normal distribution will always exhibit a bell shape:

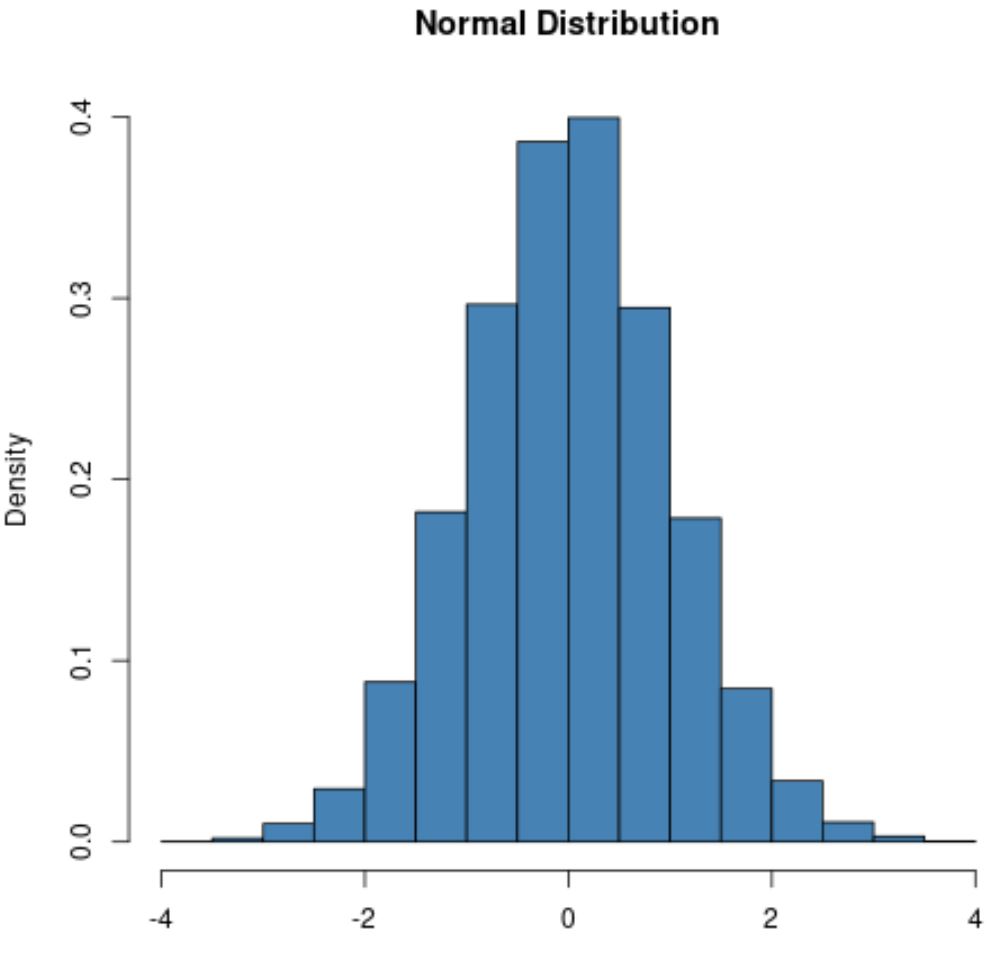
However, the shape of the Poisson distribution will vary based on the mean value of the distribution.

For example, a Poisson distribution with a small value for the mean like μ = 3 will be highly :

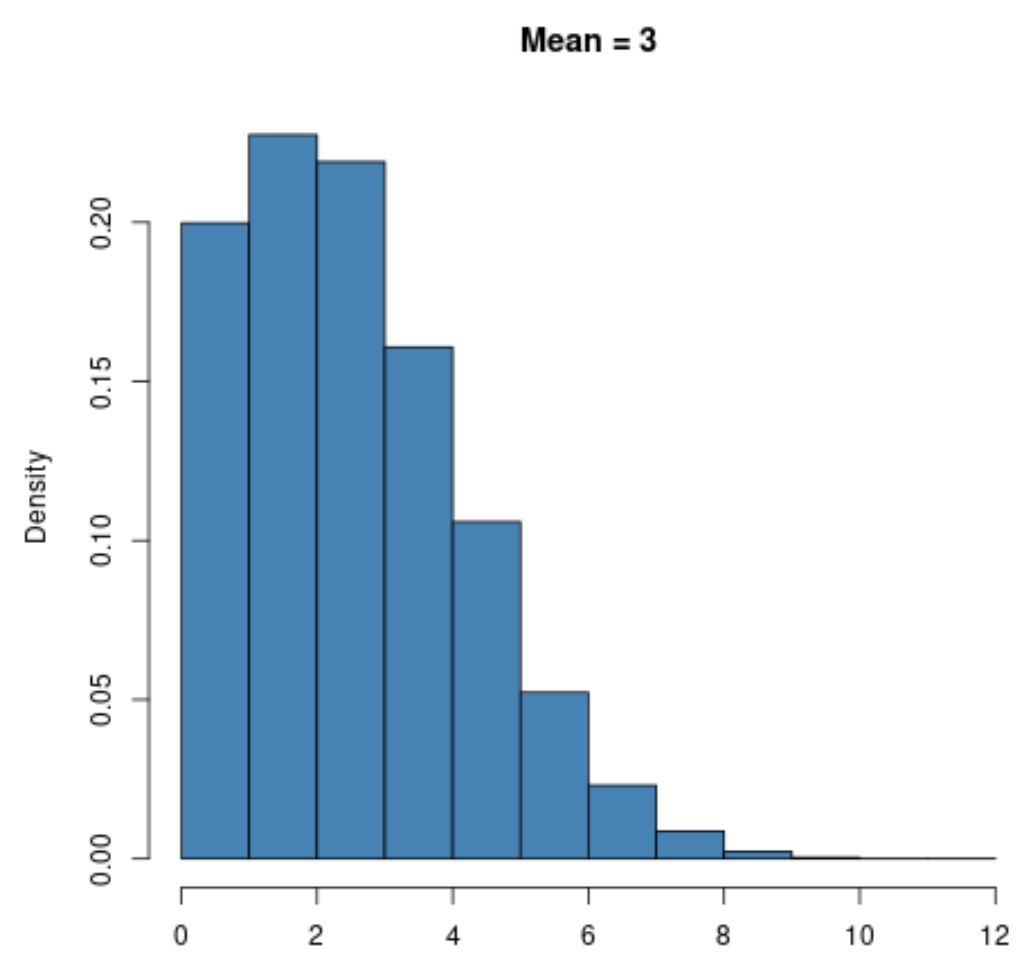
However, a Poisson distribution with a larger value for the mean like μ = 20 will exhibit a bell shape just like the normal distribution:

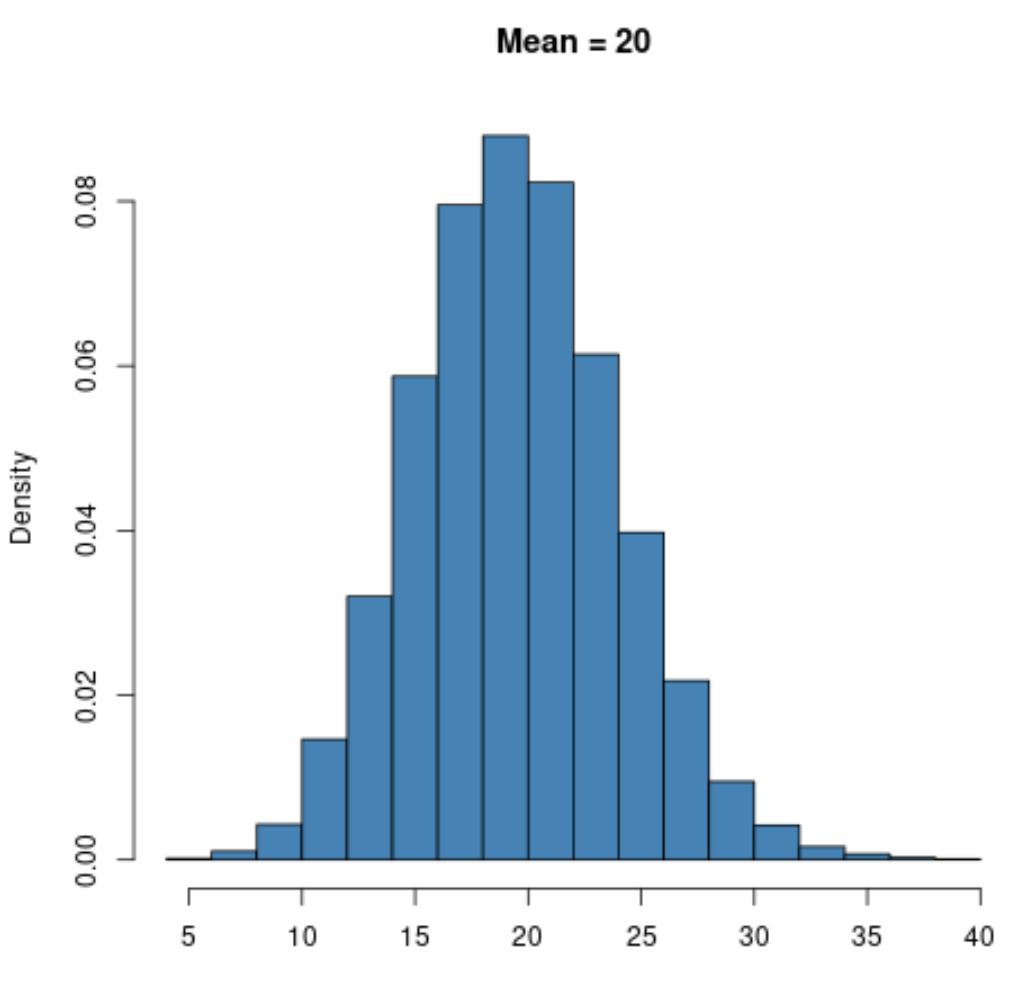
Notice that the lower bound for a Poisson distribution will always be zero no matter what the value for the mean is because a Poisson distribution can only be used with integer values that are equal to or greater than zero.

The following tutorials provide additional information about the Poisson distribution:

The following tutorials provide additional information about the normal distribution: