Table of Contents
The basic set operations, namely union, intersection, complement, and difference, are fundamental concepts in set theory that allow for manipulation and comparison of sets.
The union of two sets, denoted by the symbol “∪”, results in a new set that contains all the elements that are present in either of the original sets. For example, the union of sets A = {1, 2, 3} and B = {3, 4, 5} would be A ∪ B = {1, 2, 3, 4, 5}.
The intersection of two sets, denoted by the symbol “∩”, results in a new set that contains only the elements that are common to both of the original sets. For example, the intersection of sets A = {1, 2, 3} and B = {3, 4, 5} would be A ∩ B = {3}.
The complement of a set, denoted by the symbol “c” or “‘ “, is the set of all elements that are not present in the original set. For example, the complement of set A = {1, 2, 3} would be A’ = {4, 5}.
The difference between two sets, denoted by the symbol “\”, results in a new set that contains all the elements that are present in the first set but not in the second set. For example, the difference of sets A = {1, 2, 3} and B = {3, 4, 5} would be A B = {1, 2}.
These basic set operations are defined by specific rules and properties that allow for their use in various mathematical and logical operations. They are essential tools in set theory and have applications in various fields such as computer science, statistics, and mathematics.
Set Operations: Union, Intersection, Complement, and Difference
A set is a collection of items.
We denote a set using a capital letter and we define the items within the set using curly brackets. For example, suppose we have some set called “A” with elements 1, 2, 3. We would write this as:
A = {1, 2, 3}
This tutorial explains the most common set operations used in probability and statistics.
Union

Definition: The union of sets A and B is the set of items that are in either A or B.
Notation: A ∪ B
Examples:
- {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
- {1, 2} ∪ {1, 2} = {1, 2}
- {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
Intersection
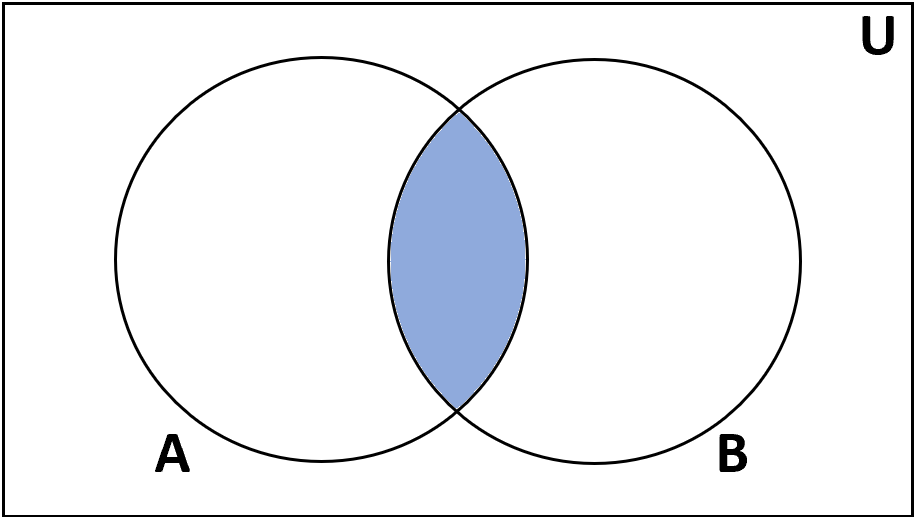
Definition: The intersection of sets A and B is the set of items that are in both A and B.
Notation: A ∩ B
Examples:
- {1, 2, 3} ∩ {4, 5, 6} = {∅}
- {1, 2} ∩ {1, 2} = {1, 2}
- {1, 2, 3} ∩ {3, 4} = {3}
Complement

Definition: The complement of set A is the set of items that are in the universal set U but are not in A.
Notation: A’ or Ac
Examples:
- If U = {1, 2, 3, 4, 5, 6} and A = {1, 2}, then Ac = {3, 4, 5, 6}
- If U = {1, 2, 3} and A = {1, 2}, then Ac = {3}
Difference
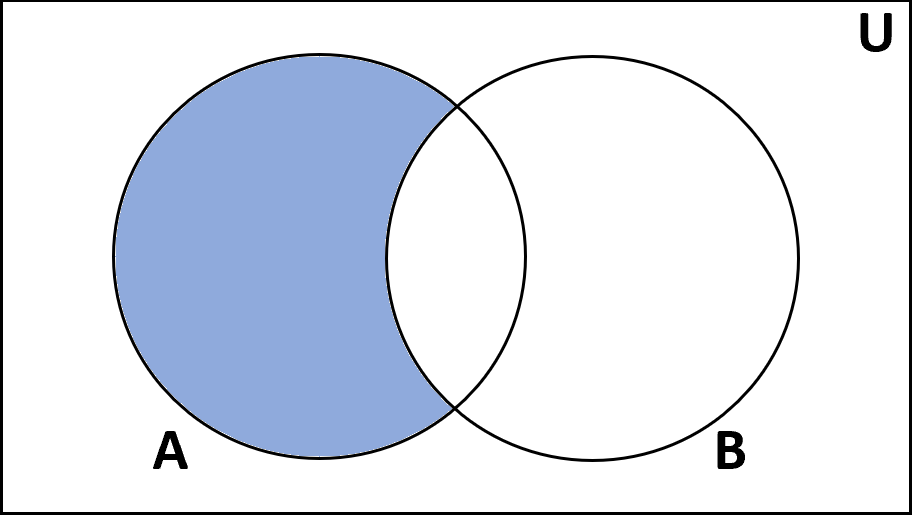
Definition: The difference of sets A and B is the set of items that are in A but not B.
Notation: A – B
Examples:
- {1, 2, 3} – {2, 3, 4} = {1}
- {1, 2} – {1, 2} = {∅}
- {1, 2, 3} – {4, 5} = {1, 2, 3}
Symmetric Difference

Definition: The symmetric difference of sets A and B is the set of items that are in either A or B, but not in both.
Notation: A Δ B
Examples:
- {1, 2, 3} Δ {2, 3, 4} = {1, 4}
- {1, 2} Δ {1, 2} = {∅}
- {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}
Cartesian Product
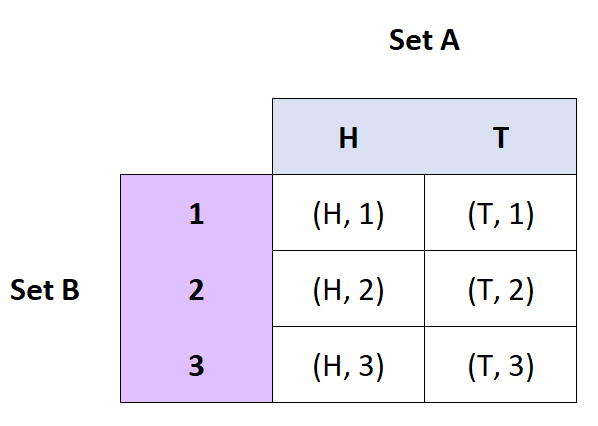
Definition: The cartesian product of sets A and B is the set of ordered pairs from A and B.
Notation: A x B
Examples:
- If A = {H, T} and B = {1, 2, 3}, then A x B = {(H, 1), (H, 2), (H, 3), (T, 1), (T, 2), (T, 3)}
- If A = {T, H} and B = {1, 2, 3}, then A x B = {(T, 1), (T, 2), (T, 3), (H, 1), (H, 2), (H, 3)}
