Table of Contents
The process of calculating SST, SSR, and SSE in Excel involves utilizing the built-in statistical functions and formulas provided by the software. SST (Total Sum of Squares) represents the total variation in a set of data, SSR (Regression Sum of Squares) measures the amount of variation explained by the regression model, and SSE (Error Sum of Squares) reflects the unexplained or residual variation. To calculate these measures, one must first input the data into an Excel spreadsheet and then use the appropriate functions, such as SUM, SUMSQ, and COUNT, to calculate the necessary values. Once these values are obtained, the formulas for SST, SSR, and SSE can be applied to calculate the respective sums. This process allows for a comprehensive analysis of the variation in a set of data and is a useful tool for statistical analysis and modeling.
Calculate SST, SSR, and SSE in Excel
We often use three different values to measure how well a actually fits a dataset:
1. Sum of Squares Total (SST) – The sum of squared differences between individual data points (yi) and the mean of the response variable (y).
- SST = Σ(yi – y)2
2. Sum of Squares Regression (SSR) – The sum of squared differences between predicted data points (ŷi) and the mean of the response variable(y).
- SSR = Σ(ŷi – y)2
3. Sum of Squares Error (SSE) – The sum of squared differences between predicted data points (ŷi) and observed data points (yi).
- SSE = Σ(ŷi – yi)2
The following step-by-step example shows how to calculate each of these metrics for a given regression model in Excel.
Step 1: Create the Data
First, let’s create a dataset that contains the number of hours studied and exam score received for 20 different students at a certain school:

Step 2: Fit a Regression Model
Along the top ribbon in Excel, click the Data tab and click on Data Analysis. If you don’t see this option, then you need to first .

Once you click on Data Analysis, a new window will pop up. Select Regression and click OK.
In the new window that appears, fill in the following information:

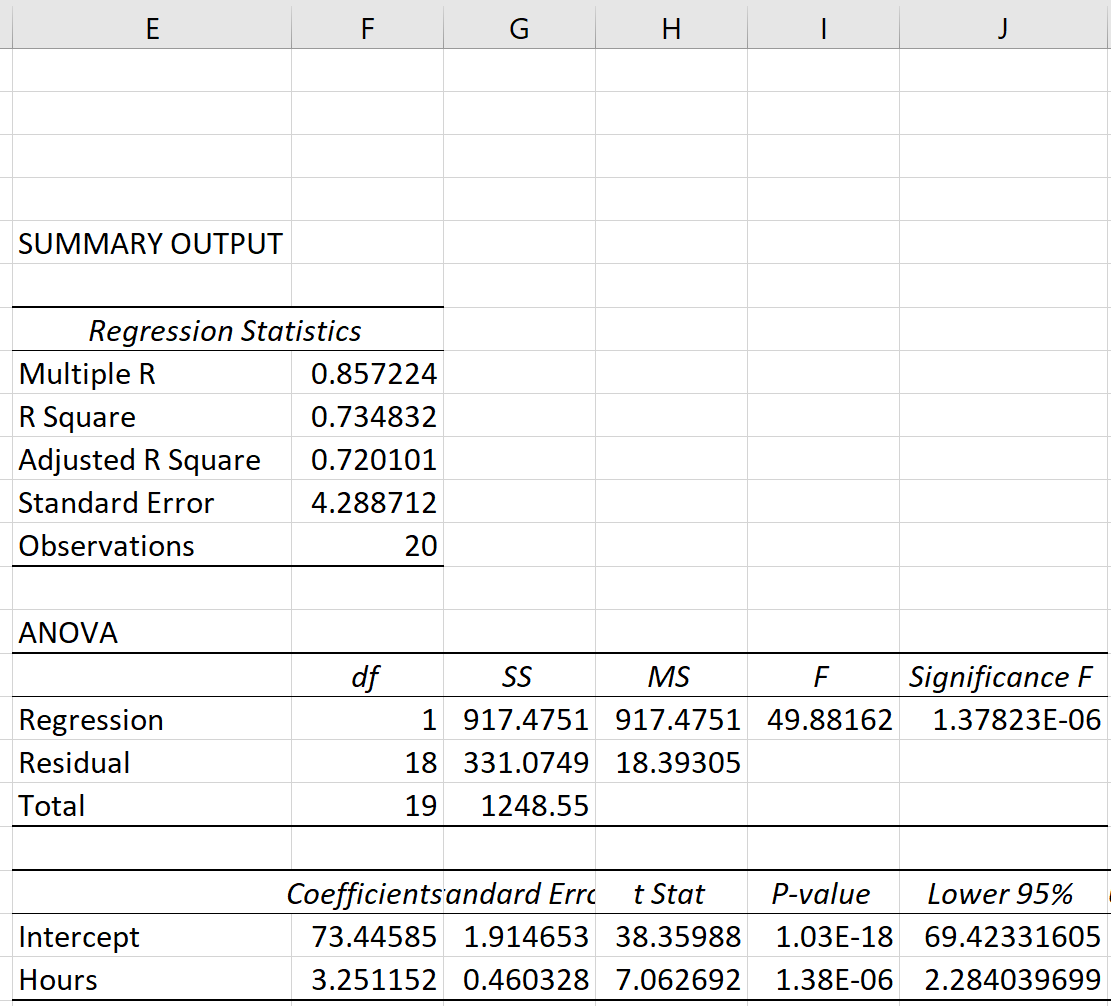
Step 3: Analyze the Output
The three sum of squares metrics – SST, SSR, and SSE – can be seen in the SS column of the ANOVA table:

The metrics turn out to be:
- Sum of Squares Total (SST): 1248.55
- Sum of Squares Regression (SSR): 917.4751
- Sum of Squares Error (SSE): 331.0749
We can verify that SST = SSR + SSE:
- SST = SSR + SSE
- 1248.55 = 917.4751 + 331.0749
We can also manually calculate the of the regression model:
- R-squared = SSR / SST
- R-squared = 917.4751 / 1248.55
- R-squared = 0.7348
This tells us that 73.48% of the variation in exam scores can be explained by the number of hours studied.
