Table of Contents
The Mann-Kendall Trend Test is a non-parametric statistical test used to determine if there is a monotonic trend in a given dataset. It can be performed in Python using the SciPy package. The Mann-Kendall test requires the data to be sorted in ascending order, then calculates the Kendall Tau correlation coefficient of the sorted data. If the correlation coefficient is greater than zero, the null hypothesis of no monotonic trend can be rejected. Otherwise, the null hypothesis that there is no trend is accepted.
A Mann-Kendall Trend Test is used to determine whether or not a trend exists in time series data. It is a non-parametric test, meaning there is no underlying assumption made about the normality of the data.
The hypotheses for the test are as follows:
H0 (null hypothesis): There is no trend present in the data.
HA (alternative hypothesis): A trend is present in the data. (This could be a positive or negative trend)
If the p-value of the test is lower than some significance level (common choices are 0.10, 0.05, and 0.01), then there is statistically significant evidence that a trend is present in the time series data.
This tutorial explains how to perform a Mann-Kendall Trend Test in Python.
Example: Mann-Kendall Trend Test in Python
To perform a Mann-Kendall Trend Test in Python, we will first install the package:
pip install pymannkendall
Once we’ve installed this package, we can perform the Mann-Kendall Trend Test on a set of time series data:
#create dataset data = [31, 29, 28, 28, 27, 26, 26, 27, 27, 27, 28, 29, 30, 29, 30, 29, 28] #perform Mann-Kendall Trend Test import pymannkendall as mk mk.original_test(data) Mann_Kendall_Test(trend='no trend', h=False, p=0.422586268671707, z=0.80194241623, Tau=0.147058823529, s=20.0, var_s=561.33333333, slope=0.0384615384615, intercept=27.692307692)
Here is how to interpret the output of the test:
- trend: This tells the trend. Possible output includes increasing, decreasing, or no trend.
- h: True if trend is present. False if no trend is present.
- p: The p-value of the test.
- z: The normalize test statistic.
- Tau: Kendall Tau.
- s: Mann-Kendal’s score
- var_s: Variance S
- slope: Theil-Sen estimator/slope
- intercept: Intercept of Kendall-Theil Robust Line
The main value we’re interested in is the p-value, which tells us whether or not there is a statistically significant trend in the data.
In this example, the p-value is 0.4226 which is not less than .05. Thus, there is no significant trend in the time series data.
Along with performing the Mann-Kendall Trend test, we can create a quick line plot using Matplotlib to visualize the actual time series data:
import matplotlib.pyplot as plt plt.plot(data)
timese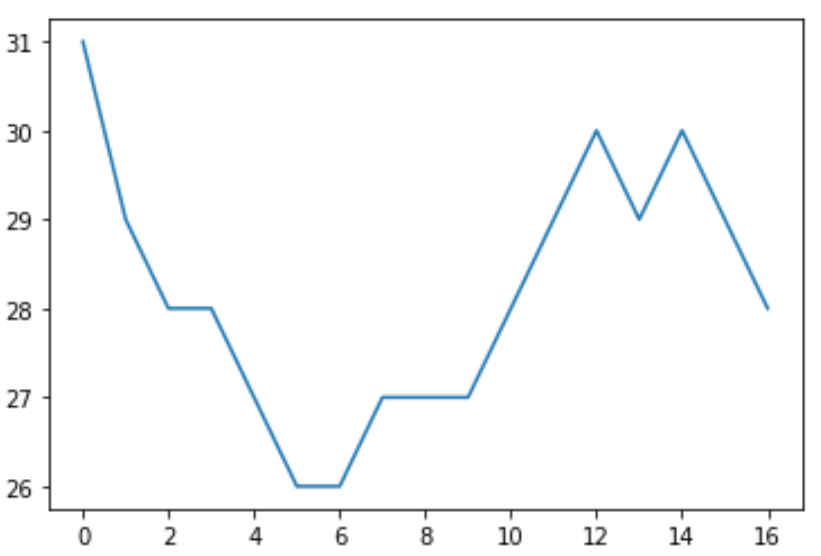
From the plot we can see that the data is a bit all over the place, which confirms that there is no clear trend in the data.
