Table of Contents
The invNorm function on a TI-84 calculator is used to find the z-score corresponding to a given area under the normal distribution curve. This is useful for statistical calculations and hypothesis testing. To use the invNorm function, first navigate to the DISTR menu by pressing the “2ND” and “VARS” buttons. Then select “3: invNorm(” and enter the desired area in decimal form. The calculator will return the z-score associated with that area. For example, if we want to find the z-score for an area of 0.35, we would enter “invNorm(0.35)” and the calculator would return a value of approximately -0.3853. This means that 35% of the data falls below a z-score of -0.3853. Multiple examples can be provided by entering different areas into the invNorm function and observing the corresponding z-score.
Use invNorm on a TI-84 Calculator (With Examples)
You can use the invNorm() function on a TI-84 calculator to find z critical values associated with the .
This function uses the following syntax:
invNorm(probability, μ, σ)
where:
- probability: the significance level
- μ: population mean
- σ: population standard deviation
You can access this function on a TI-84 calculator by pressing 2nd and then pressing VARS. This will take you to a DISTR screen where you can then use invNorm():

The following examples show how to use this function in practice.
Example 1: Z-Critical Value for One-Tailed Tests
Suppose a researcher is conducting a left-tailed hypothesis test using α = .05. What is the z-critical value that corresponds to this alpha level?

The answer is z = -1.64485.
Suppose a researcher is conducting a right-tailed hypothesis test using α = .05. What is the z-critical value that corresponds to this alpha level?
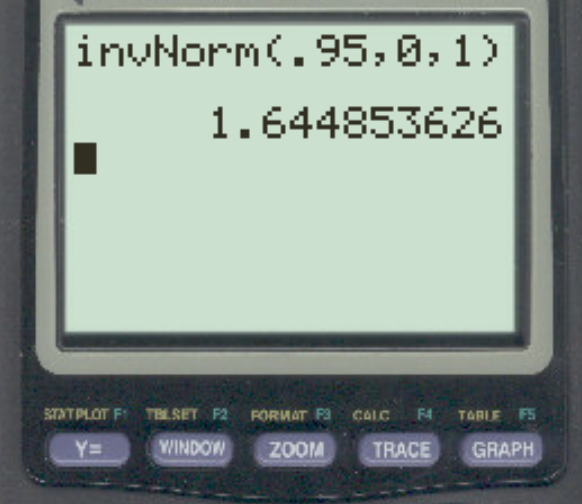
The answer is z = 1.64485.
Example 2: Z-Critical Value for Two-Tailed Tests
To find this critical value, we can use the formula 1 – α/2. In this case, we will use 1 – .05/2 = .975 for the probability:

The answer is z = 1.96.
Example 3: Z-Critical Value for Cut-Off Scores
Suppose the scores on a particular exam are normally distributed with a mean of 70 and a standard deviation of 8. What score separates the top 10% from the rest?
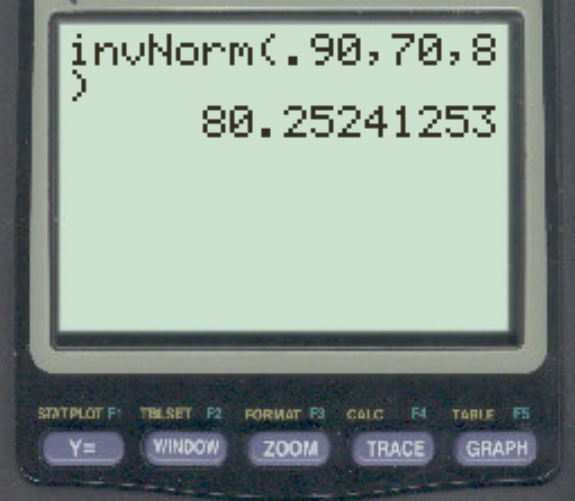
The answer is 80.25.
Suppose the heights of males in a particular city are normally distributed with a mean of 68 inches and a standard deviation of 4 inches. What height separates the bottom 25% from the rest?

The answer is 65.3 inches.
