Table of Contents
Standard deviation is a measure of how spread out a set of data is from its mean. It is often used to compare the variability of different data sets. To compare standard deviations, one can calculate the standard deviation for each data set and then compare them. The data set with a larger standard deviation would have a wider range of values and therefore be more spread out. For example, if we have two sets of test scores, one with a standard deviation of 5 and the other with a standard deviation of 10, we can conclude that the second set has a greater variability in scores. This information can be useful in determining the consistency and reliability of data sets and in making informed decisions based on the level of variability.
Compare Standard Deviations (With Example)
Often you may want to compare standard deviations between two datasets to determine if they are equal.
The most common way to compare standard deviations is to actually compare the variances (the standard deviation squared) between two datasets using one of the following methods:
Method 1: Use Rule of Thumb
One crude way to determine if two variances are equal is to use the variance rule of thumb.
As a rule of thumb, if the ratio of the larger variance to the smaller variance is less than 4 then we can assume the variances are approximately equal.
Otherwise, if the ratio is equal to or greater than 4, we assume that the variances are not equal.
Method 2: Use Formal Statistical Test
A more formal way to test if two variances are equal is to use an F-test.
This test uses the following hypotheses:
- H0: σ12 = σ22 (the population variances are equal)
- H1: σ12 ≠ σ22 (the population variances are not equal)
To perform an F-test, we typically use statistical software such as R, Python, Excel, SPSS, etc.
The following examples show how to use each method in practice to compare the standard deviations between the following two datasets that show the exam scores received by students who used two different study methods to prepare for the exam:

Method 1: Use Rule of Thumb to Compare Standard Deviations
One way to compare the standard deviations between the two datasets is to first calculate the variance of each dataset:
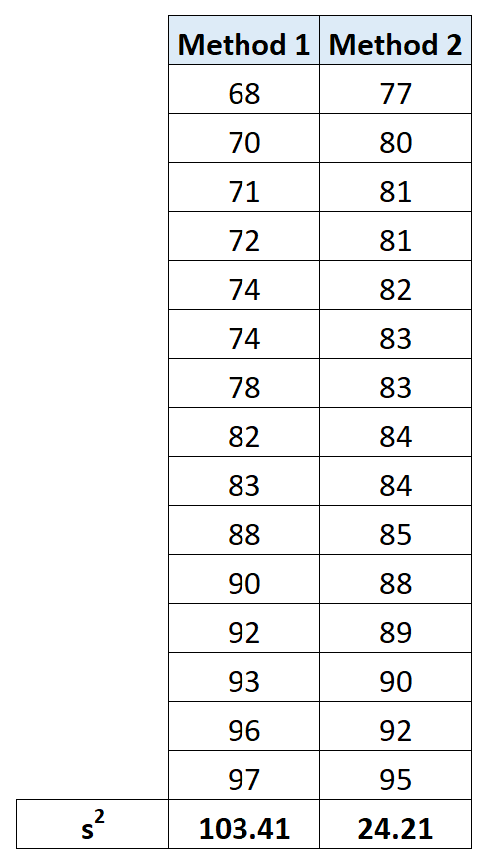
Next, we can calculate the ratio of the larger variance to the smaller variance:
Since this ratio is greater than 4, we would assume that the variances are not equal.
Thus, we would assume that the standard deviations between the two datasets are not equal.
Method 2: Use F-Test to Compare Standard Deviations
Another way to compare the standard deviations between the two datasets is to perform an F-test.
Most statistical software is able to perform an F-test, but we will use the following code in R to do so:
#enter exam scores for both groups of students method1 <- c(68, 70, 71, 72, 74, 74, 78, 82, 83, 88, 90, 92, 93, 96, 97) method2 <- c(77, 80, 81, 81, 82, 83, 83, 84, 84, 85, 88, 89, 90, 92, 95) #perform an F-test to determine if the variances are equal var.test(method1, method2) F test to compare two variances data: method1 and method2 F = 4.2714, num df = 14, denom df = 14, p-value = 0.01031 alternative hypothesis: true ratio of variances is not equal to 1 95 percent confidence interval: 1.434049 12.722857 sample estimates: ratio of variances 4.27144
The F-test returns the following results:
- F-test statistic: 4.2714
- p-value: .01031
Recall that the F-test uses the following hypotheses:
- H0: σ12 = σ22 (the population variances are equal)
- H1: σ12 ≠ σ22 (the population variances are not equal)
Since the p-value of our test (.01031) is less than .05, we have sufficient evidence to reject the null hypothesis.
We would conclude that the variances are not equal.
Thus, we would conclude that the standard deviations between the two datasets are not equal.
Bonus: You can also use the Statology to perform this F-test.
Additional Resources
The following tutorials provide additional information about using standard deviations in statistics:
