Can you create a Confidence Interval Using the F Distribution?

---

To determine if the variances of two populations are equal, we can calculate the variance ratio σ²₁ / σ²₂, where σ²₁ is the variance of population 1 and σ²₂ is the variance of population 2.

To estimate the true population variance ratio, we typically take a from each population and calculate the sample variance ratio, s₁² / s₂², where s₁²  and s₂² are the sample variances for sample 1 and sample 2, respectively.

This test assumes that both s₁²  and s₂² are computed from independent samples of size n₁ and n₂, both drawn from normally distributed populations.

The further this ratio is from one, the stronger the evidence for unequal population variances. 

The (1-α)100% confidence interval for σ²₁ / σ²₂ is defined as:

(s₁²  / s₂²) * F_{n1-1, n2-1, α/2}   ≤  σ²₁ / σ²₂  ≤  (s₁²  / s₂²) * F_{n2-1, n1-1, α/2}

where F_{n2-1, n1-1, α/2} and F_{n1-1, n2-1, α/2} are the critical values from the F distribution for the chosen significance level α.

The following examples illustrate how to create a confidence interval for σ²₁ / σ²₂ using three different methods:

• By hand
• Using Microsoft Excel
• Using the statistical software R

For each of the following examples, we will use the following information:

• α = 0.05
• n₁ = 16
• n₂ = 11
• s₁² =28.2
• s₂² = 19.3

Creating a Confidence Interval By Hand

To calculate a confidence interval for σ²₁ / σ²₂ by hand, we’ll simply plug in the numbers we have into the confidence interval formula:

(s₁²  / s₂²) * F_{n1-1, n2-1,α/2}   ≤  σ²₁ / σ²₂  ≤  (s₁²  / s₂²) * F_{n2-1, n1-1, α/2}

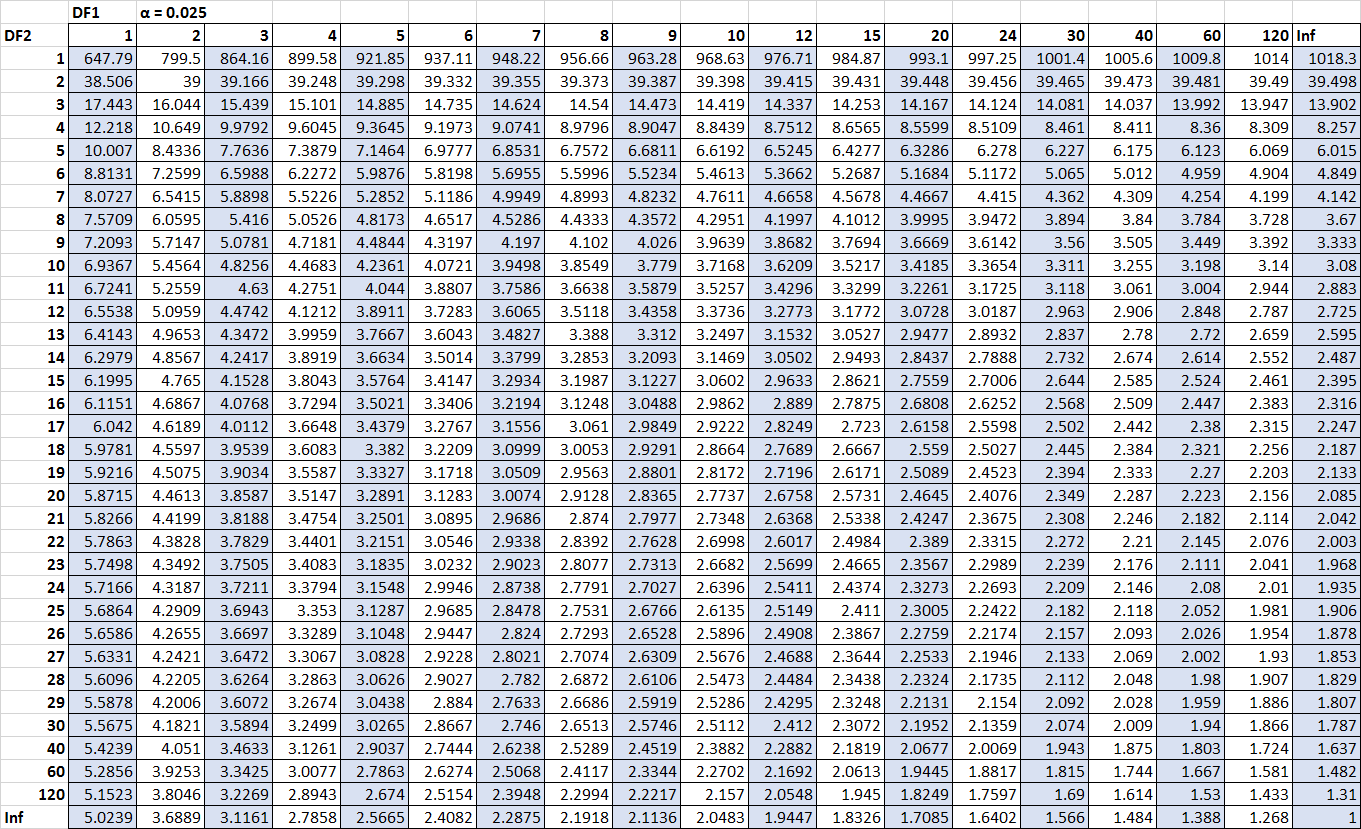
The only numbers we’re missing are the critical values. Luckily, we can locate these critical values in :

F_{n2-1, n1-1, α/2}   = F_{10, 15, 0.025}   = 3.0602

F_{n1-1, n2-1, α/2}  =  1/ F_{15, 10, 0.025} = 1 / 3.5217 = 0.2839

Now we can plug all of the numbers into the confidence interval formula:

(s₁²  / s₂²) * F_{n1-1, n2-1,α/2}   ≤  σ²₁ / σ²₂  ≤  (s₁²  / s₂²) * F_{n2-1, n1-1, α/2}

(28.2 / 19.3) * (0.2839) ≤  σ²₁ / σ²₂  ≤  (28.2 / 19.3) * (3.0602)

0.4148 ≤  σ²₁ / σ²₂  ≤  4.4714

Thus, the 95% confidence interval for the ratio of the population variances is (0.4148, 4.4714).

Creating a Confidence Interval Using Excel

The following image shows how to calculate a 95% confidence interval for the ratio of population variances in Excel. The lower and upper bounds of the confidence interval are displayed in column E and the formula used to find the lower and upper bounds are displayed in column F:

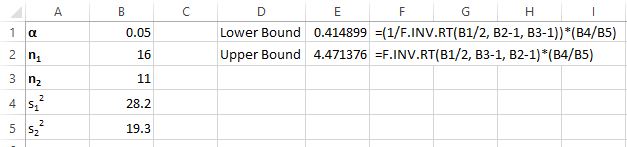
Thus, the 95% confidence interval for the ratio of the population variances is (0.4148, 4.4714). This matches what we got when we calculated the confidence interval by hand.

Creating a Confidence Interval Using R

The following code illustrates how to calculate a 95% confidence interval for the ratio of population variances in R:

#define significance level, sample sizes, and sample variances
alpha <- .05
n1    <- 16
n2    <- 11
var1  <- 28.2
var2  <- 19.3

#define F critical values
upper_crit <- 1/qf(alpha/2, n1-1, n2-1)
lower_crit <- qf(alpha/2, n2-1, n1-1)

#find confidence interval
lower_bound <- (var1/var2) * lower_crit
upper_bound <- (var1/var2) * upper_crit

#output confidence interval
paste0("(", lower_bound, ", ", upper_bound, " )")

#[1] "(0.414899337980266, 4.47137571035219 )"

Thus, the 95% confidence interval for the ratio of the population variances is (0.4148, 4.4714). This matches what we got when we calculated the confidence interval by hand.